模型选择 Model Selection
过拟合和欠拟合 Overfitting and Underfitting
这个其实非常好解释, 就放在一起说了.
过拟合就像是平时做很多作业题但是却不会考试的学生, 一到考试就拉胯, 但是平时作业写得很完美. 过拟合导致了过度的学习了作业中的内容, 甚至是单纯错误的把作业题背下来了, 导致失去了泛化能力.
欠拟合就像是平时不怎么学习的学渣. 考试题也不会, 作业也不会写. 欠拟合根本没有对作业中的内容进行学习, 对考试题型的拟合程度根本不够.
欠拟合对应着高偏差, 过拟合对应着高方差.
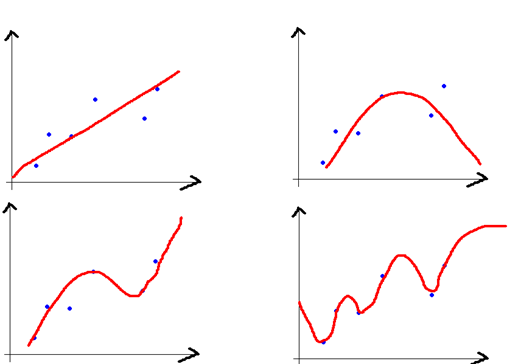
- 左上的模型偏差最大, 右下的模型偏差最小.
- 左上的模型方差最小, 右下的模型方差最大. 这样去理解, 如果两个训练集的分布有一丝丝差异, 由于采用了复杂的模型拟合, 会导致分类结果或回归结果截然不同. 就导致新样本点散落在原样本的两侧, 方差极高.
用CV代表在验证集上的训练误差, 而Training error代表在训练集上的训练误差.
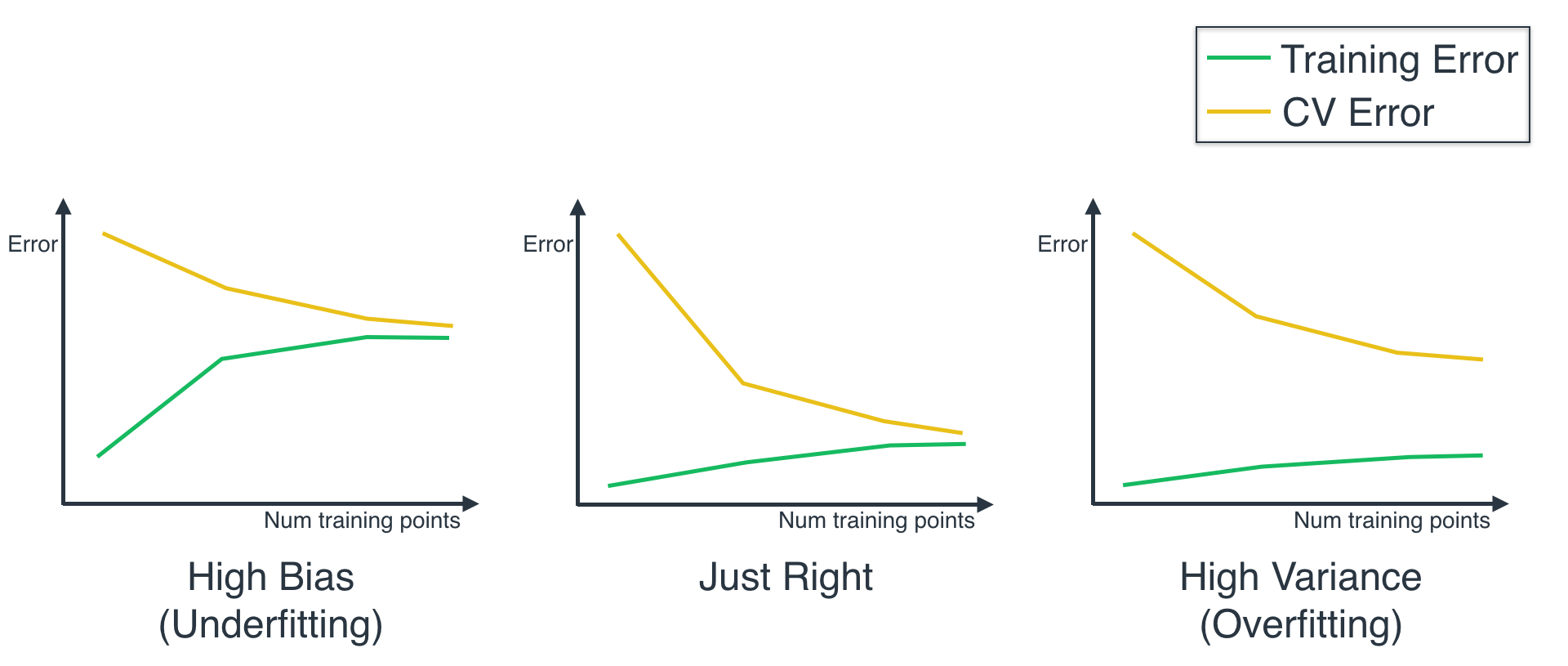
欠拟合的训练误差和验证误差都很大, 过拟合的训练误差很小, 但是测试误差很大. 只有在中间的模型刚刚好, 具有泛化能力, 也同时具有判断问题的能力.
交叉验证 Cross Validation
先解释一下数据的分割问题. 我们常常将数据分割为三类, 分别是训练集, 验证集, 和测试集. 一般都将一份数据集按照比例划分成训练集和验证集, 测试集一般取样于实际问题中, 这样才能够检验模型真正的泛化能力. 但是在后面说的”全部数据集” 都是在不考虑测试集情况下说的, 也就是只划分为训练集和测试集的情况.
| 划分 | 意义 |
|---|---|
| 训练集 | 专门用来训练模型的, 在训练过程中, 模型参数会随着训练而改变, 就像是上课一样. |
| 验证集 | 用来检测当前模型对数据集的拟合程度, 此时模型参数不会更新, 它像作业题. |
| 测试集 | 模型从来没有见过的, 真正的考试题, 能够判决模型能力的终极手段. |
测试集只能用一次, 就是最后对模型参数调好后进行终极测试的时候.
对于一份数据, 如果我们既将它全部用来训练, 也用于验证, 那么就相当于用作业题去上课, 造成了标签泄露. 如果只将训练集拿去训练呢, 又会损失一部分训练的数据, 并且模型最终的结果严重取决于训练集和验证集的划分. 基于这个矛盾, 提出了交叉验证.
K折交叉验证 K-Fold Cross Validation
将含有$m$个样本的数据集划分为$k$个不相交的子集, 每个子集有$\frac{m}{k}$ 个样本. 从每次分好的样本中, 选一个子集作为验证集, 其他$k-1$个子集全部作为训练集, 每次训练都能得到一个评估值(每次都用同样的参数训练一个新的分类器), 重复进行$k$ 次最后取平均, 就是k折交叉验证所得到的验证结果. K-Fold CV 能反映出当前模型真正的拟合能力, 经验值常取k为5, 10…
留一法 Leave-one-out cross-validation
当$k=m$的时候, 每个子集只有一个样本, 每次只取一个样本作为验证集, 用其余所有样本进行训练, K折交叉验证就变成了留一法. 留一法能够最大程度的利用样本, 但是也同时牺牲了时间. 如果有k个样本, 则需要训练k次, 测试k次. 小样本适用.
网格搜索 Grid Search
当我们不知道模型的参数如何选择时, 可以采用网格搜索. 网格搜索其实就是暴力穷举, 将模型所有可能的参数取值全都试一遍, 这能保证不遗漏模型组合参数造成的影响, 但是同时这样做的时间成本也非常高. 所以一般情况下都是先进行参数范围的缩小, 最后再使用网格搜索. 网格搜索也常和交叉验证一起使用, 用来更精确的评价模型.


