本文前置知识:
- BERT: 详见ELMo, GPT, BERT.
SpanBERT: Improving Pre-training by Representing and Predicting Spans
本文是论文SpanBERT: Improving Pre-training by Representing and Predicting Spans的阅读笔记和个人理解.
Basic Idea
作者认为, 许多NLP任务中所涉及到的推理任务是关于多个Text Token之间的, 而非基于单个Token之间的.
例如, 在回答问题Which NFL team won Super Bowl 50?时, 直接给出答案Denver Broncos比在Denver后给出Broncos要困难的多, 但前者却更贴近与现实场景, 难度也更大.
作者尝试提出SpanBERT来解决这种Span Level Prediction的问题.
SpanBERT
SpanBERT通过三种方式来帮助模型理解语言:
- 将Token Level Mask替换为Span Level Mask.
- 引入一种新的辅助目标来SBO帮助模型训练.
- 只使用单个句子训练, 而非BERT所使用的句子对.
Span Masking
在BERT中, 对于给定的输入序列$X=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$, 其编码表示为:
$$
\operatorname{enc}\left(x_{1}, x_{2}, \ldots, x_{n}\right)=\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{n}
$$
但在BERT中, 打Mask是对单个Token做的. 在SpanBERT中, 作者使用Span Level的Mask, 对一连串的Token做指定长度的Mask. 通过均匀分布随机采样得到Span Mask的初始位置.
而Span Mask的长度是通过迭代随机采样的来的, 继续扩展Span的几率服从几何分布$\ell \sim \operatorname{Geo}(p=0.2)$, 最大的Span长度$\ell_{\max }=10$. 即连续采样, 每次都有$p=0.2$ 的几率继续扩展Span, 每次都有$q = 1 - p = 0.8$ 的几率停止扩展Span. 其概率分布如下:
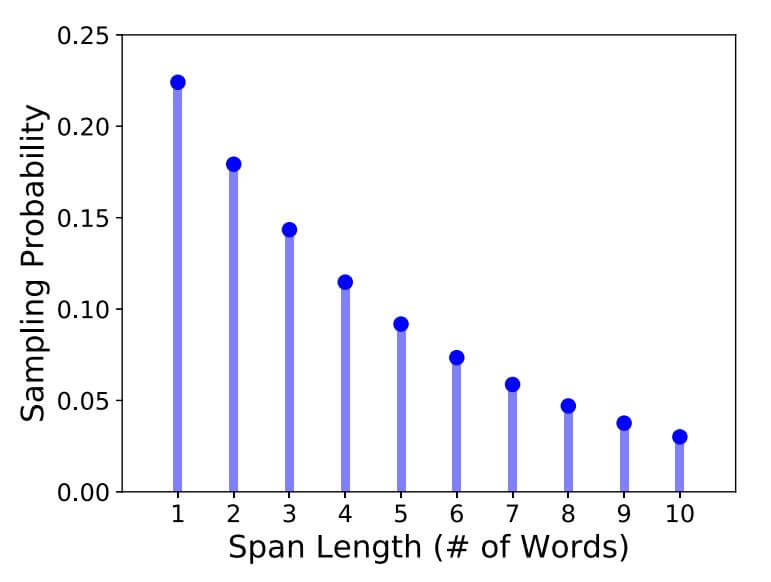
那么Span长度的期望值为3.8, 其推导过程如下:
$$
\begin{aligned}
&p = 0.2 \\
&q = 1 - p = 0.8 \\
&p^\prime = \frac{p}{1-q^{10}} = 0.224 \\
\end{aligned}
$$
$p^\prime$ 代表Span最大长度为10以下的概率的归一化. $1-q^{10}$ 为当前Span不超过10的概率和, 需要用$p$ 去除以这个值, 让$p^\prime$ 排除掉Span长度大于10的情况.
参考SpanBert:对 Bert 预训练的一次深度探索的评论区.
故限定Span最大长为10的期望为:
$$
\begin{aligned}
E(x) &= p^\prime \sum_{n=1}^{10}n q^{n-1} \\
&= p^\prime (1 + 2q + 3q^2 + \dots + 10q^9) \\
&= 0.224 \cdot 16.9469=3.797 \approx3.8
\end{aligned}
$$
即Span长度期望为3.8, 如果向上取整就是4.
Span Masking将Token Level的Mask变更为了Span Level的Mask, 任务的训练难度更为复杂.
Span Boundary Objective
作者希望Span的结尾能尽可能多的表示出Span内部的内容, 因此作者直接引入一个新的辅助目标来实现.
SBO的提出应该也受到一些其他模型的启发, 例如ERNIE(Baidu), BERT WWM等模型, 都是基于Span Level Mask做的额外处理.
对于Span外部的起始边界和结束边界$(s, e)$, 作者希望通过某种方式$f(\cdot)$, 来根据其边界两侧的表示$\mathbf{x}_{s-1}, \mathbf{x}_{e+1}$, 以及每个Span内部的Token $x_i$ 所对应的位置编码$\mathbf{p}_{i-s+1}$ 来得到预测结果$\mathbf{y}_i$, 从而预测出Span内的每个Token:
$$
\mathbf{y}_{i}=f\left(\mathbf{x}_{s-1}, \mathbf{x}_{e+1}, \mathbf{p}_{i-s+1}\right)
$$
这里作者简单的使用两层FFN和GeLU来将$\mathbf{y}_i$ 转换为$x_i$:
$$
\begin{array}{l}
\mathbf{h}_{0}=\left[\mathbf{x}_{s-1} ; \mathbf{x}_{e+1} ; \mathbf{p}_{i-s+1}\right] \\
\mathbf{h}_{1}=\text { LayerNorm }\left(\operatorname{GeLU}\left(\mathbf{W}_{1} \mathbf{h}_{0}\right)\right) \\
\mathbf{y}_{i}=\text { LayerNorm }\left(\operatorname{GeLU}\left(\mathbf{W}_{2} \mathbf{h}_{1}\right)\right)
\end{array}
$$
$[\cdot]$ 代表拼接操作.
SBO将和MLM的损失函数共同优化, 二者之间是简单的加和关系即可:
$$
\begin{aligned}
\mathcal{L}\left(x_{i}\right) &=\mathcal{L}_{\mathrm{MLM}}\left(x_{i}\right)+\mathcal{L}_{\mathrm{SBO}}\left(x_{i}\right) \\
&=-\log P\left(x_{i} \mid \mathbf{x}_{i}\right)-\log P\left(x_{i} \mid \mathbf{y}_{i}\right)
\end{aligned}
$$
那么根据SBO, 模型可能会学到一些关于Span的内容, 因为SBO要求模型必须用边界信息来猜Span内部指定位置的内容.
下面给出一个说明SBO的例子:
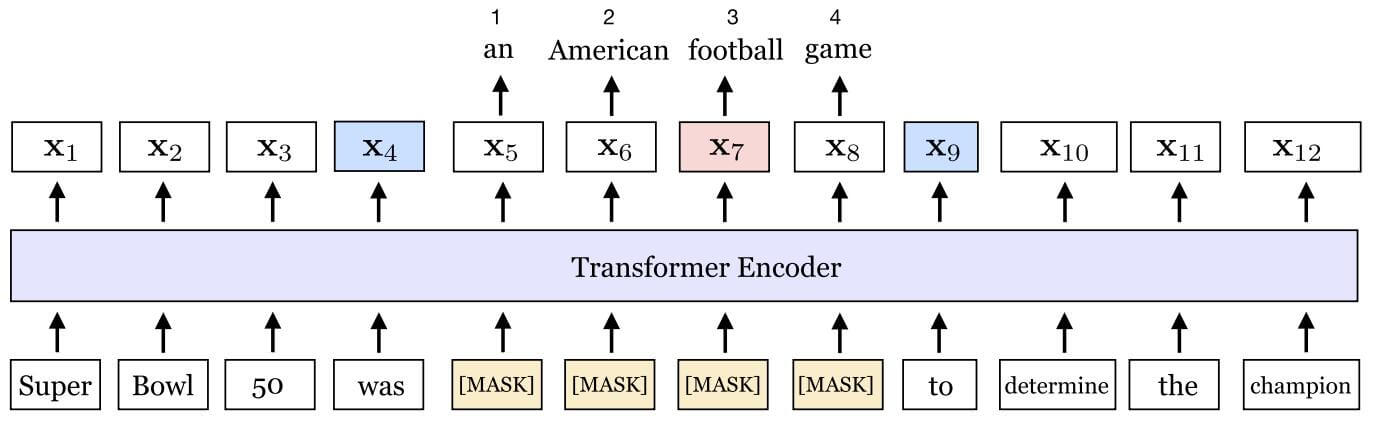
在该例中, $\text{football}$ 被选中, 将在其附近给长度为4的区域打上Mask, 这个词应该根据被Mask的区域的边界表示$\mathbf{x}_3, \mathbf{x}_9$, 以及$\text{football}$ 在Span Mask中的相对位置的编码$\mathbf{p}_3$ 共同预测出来.
所以在该例中, 损失函数为MLM预测$\text{football}$ 和SBO预测$\text{football}$ 的损失之和:
$$
\begin{aligned}
\mathcal{L}(\text { football }) &=\mathcal{L}_{\mathrm{MLM}}(\text { football })+\mathcal{L}_{\mathrm{SBO}}(\text { football }) \\
&=-\log P\left(\text { football } \mid \mathbf{x}_{7}\right)-\log P\left(\text { football } \mid \mathbf{x}_{4}, \mathbf{x}_{9}, \mathbf{p}_{3}\right)
\end{aligned}
$$
Single - Sequence Training
在SpanBERT中, 作者舍弃了BERT的句子对训练法, 仅使用单句训练, 并抛弃NSP任务, 理由如下:
- 句子对的引入限制了单句最长文本长度. 使用单句训练, 最长文本长度可以直接翻倍.
- 句子对上下不相关时, 会引入非常大的噪声.
Experiments
详细的参数设置请参照原论文.
Extractive Question Answering
抽取式QA的结果如下:

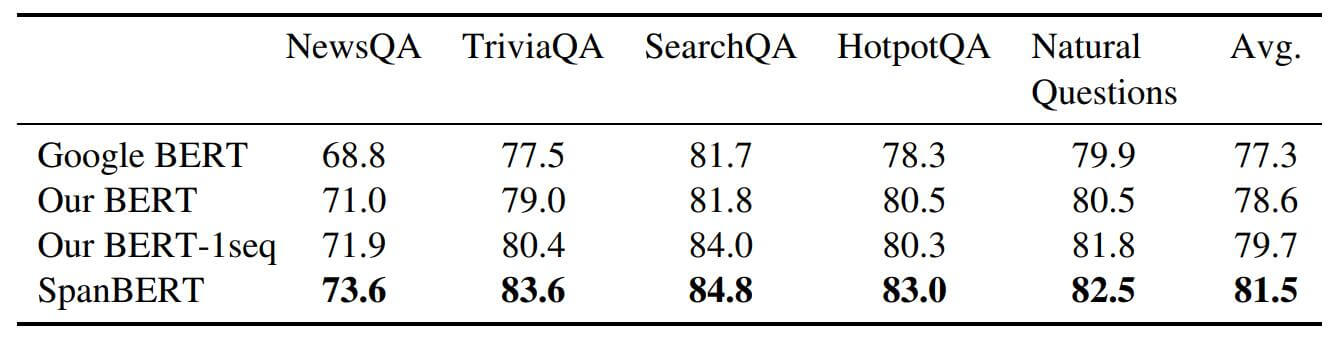
在这些数据集上的提升趋势是一致的, 每个数据集都有提升.
Coreference Resolution
指代消解的任务目标是将文本中提到的同一实体的不同表述找出来, 即将同一事物的不同自然语言描述链接到文本中的同一事物.
对指代消解任务, 每个Mention Span $x$, 它与之前文本中对应的多个定长Span $y^\prime \in Y$ 都有一个得分$s(x, y)$, 根据得分使用Softmax能够判断出$y$ 是哪个Span的指代:
$$
P(y)=\frac{e^{s(x, y)}}{\sum_{y^{\prime} \in Y} e^{s\left(x, y^{\prime}\right)}}
$$
其中Span Pair的打分函数$s(x, y)$ 是由FFN得来的:
$$
\begin{aligned}
s(x, y) &=s_{m}(x)+s_{m}(y)+s_{c}(x, y) \\
s_{m}(x) &=\mathrm{FFNN}_{m}\left(\mathbf{g}_{\mathrm{x}}\right) \\
s_{c}(x, y) &=\mathrm{FFNN}_{c}\left(\mathbf{g}_{\mathrm{x}}, \mathbf{g}_{\mathbf{y}}, \phi(x, y)\right)
\end{aligned}
$$
在这里, $\mathbf{g}_x, \mathbf{g}_y$ 代表两个Transformer提取出Span两个端点的隐态输出和Span内部的Attention的加权求和后的拼接向量, $\text{FFNN}_m, \text{FFNN}_c$ 代表两个有一层隐层的前馈神经网络, $\phi(x, y)$ 代表人工构建的特征.
和论文BERT for Coreference Resolution: Baselines and Analysis的使用方法一致, BERT系列指代消解模型是BiLSTM + Attention系列模型在C2F - Coref上的升级.
更多关于神经网络指代消解的论文, 还可以参考:
指代消解的数据集OntoNotes上表现如下:
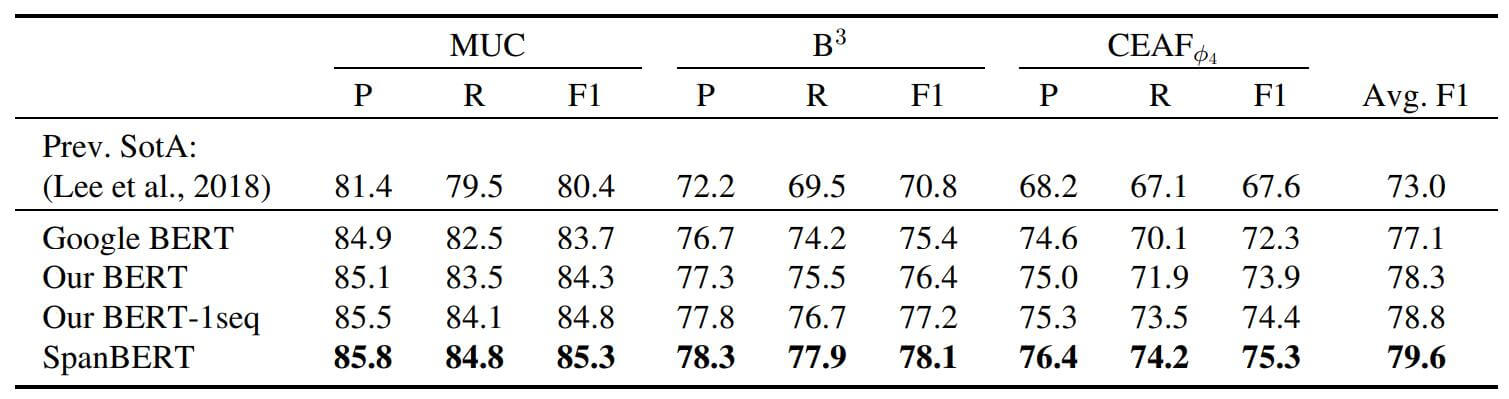
相较于其他的BERT Baseline, SpanBERT有些许提升, 并且提升在每个数据集上都是一致的.
Relation Extraction
在关系抽取的数据集TACRED上结果如下:
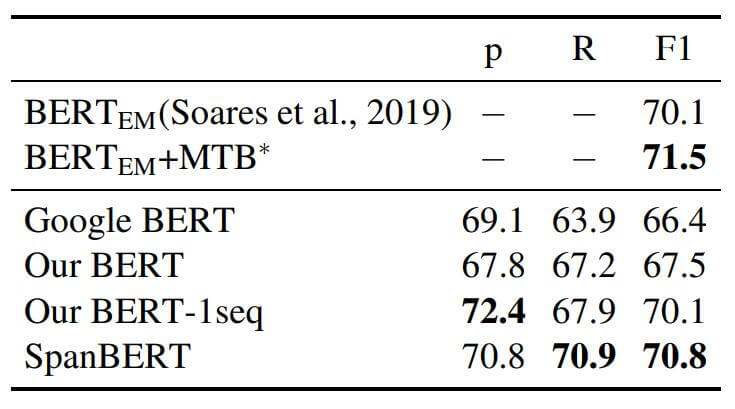
SpanBERT在关系抽取上的标现达到平均水平, 在Recall上进步比较大.
GLUE
GLUE上的结果如下:

相较于其他BERT Baseline, SpanBERT提升也是全面的. 尤其是在二分类数据集QNLI上提升比较大, 我认为这可能是SBO带来的提升.
Ablation Study
Masking Schemes
作者将Subword, Whole Words, Named Entities, Noun Phrases, Geometric Spans几种Mask策略放在一起做了对比:
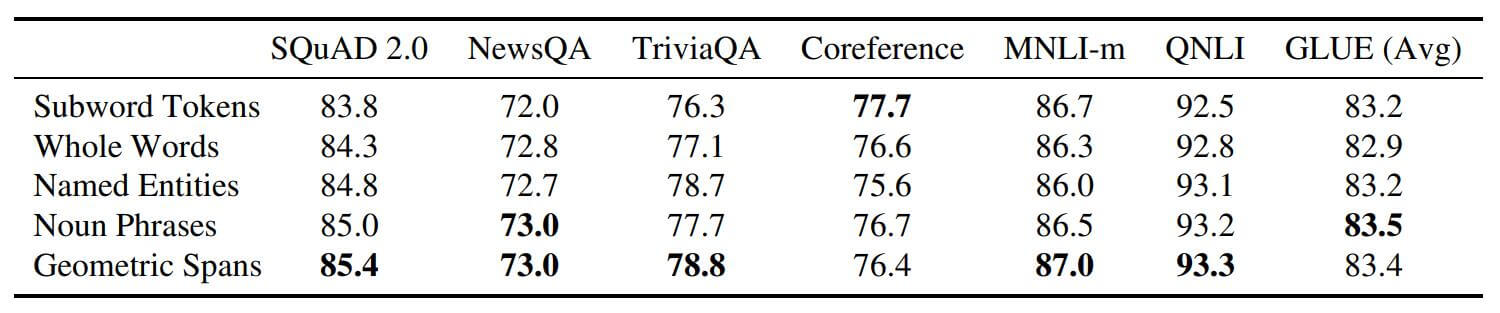
能够看出, SpanBERT中的Geometric Spans几乎是最有效的, 但在Coreference上似乎没有与其他提升一致. 但其他的策略也都不如BERT最开始使用的Subword Tokens策略要好.
Auxiliary Objectives
不同的辅助目标对Span BERT的影响如下:

如果使用NSP任务, 性能会比不使用NSP并单句训练的SpanBERT有损, 加上SBO任务后会使得Coreference上的表现大幅提升(相较于上表).
Summary
SpanBERT作为一种BERT的改进方案, 提出了更完备的Span Masking方案. SpanBERT加入了SBO任务, 使用边界信息和被Mask的Token在Span内的相对位置信息能预测出Span内部的内容. 也没有使用句子对作为训练方式, 抛弃了对性能有损害的NSP任务.
SpanBERT在各类任务上性能皆超过BERT, 应该算作是一种比较有效的改进方式, 方法也比较巧妙.
我感觉效果全面提升的原因主要是增大了模型的训练难度, 并且包含有一定的随机性, 在预测时, 需要对每个Span内的Token都做预测, 大大的强化了Span左右两端判断Span内部内容的能力, 这样比漫无目的的Mask要有效得多, 在不同的位置编码下, 需要判断Span内部不同的内容, 进一步的提高了模型对两端信息的利用率, 使得两端的隐态更有意义, 更有内容.

