2020.09.09: 叙述调整.
深度神经网络 Deep Neural Network
在本文中的神经网络是指的深度神经网络 Deep Neural Network. 进入到深度学习领域后, 除去DL计算量大, 参数多的特点外, 还会发现深度学习中有一个很大的特点: 不需要特征工程. 特征提取直接由模型自动端到端的完成. DL大多是用仿生学的结构, 来获得信息的新的表示, 所以我们也常说, 深度学习的本质是表示学习. 其强大的功能我认为是由神经网络本身对事物的表征方式和神经网络的万能逼近定理决定的.
在错杂的神经网络结构中, 对数据进行非线性拟合. 由于其结构的复杂性, DL也没有很好的解释性, 但是研究人员常常将其逐步拆开, 发现其中的规律, 看看神经网络究竟学习到了什么.
神经元 Neuron
神经元的概念这个比较简单, 神经网络是由神经元构成的. 一定都看过一张类似的图:
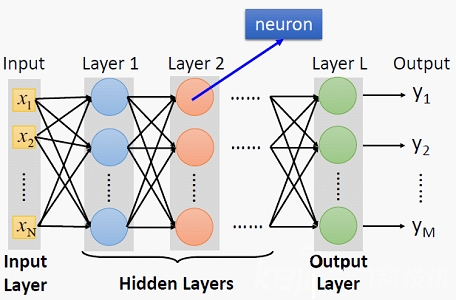
这就是神经网络的结构, 两端的分别称为输入层和输出层, 中间的称为隐藏层. 最左侧的输入层大小与输入的特征维数是保持一致的. 最右侧的输出层大小与输出的维数保持一致, 如果任务是分类任务, 输出层的神经元个数就是要分类的类别数, 预测的是归属于每类的类别概率. 如果是回归任务, 最后一层的神经元只有一个, 预测的是回归值.
在不对神经网络注入灵魂的情况下, 每个神经层之间是做最简单的线性回归, 只不过我们形象的将这个过程拆解为神经元的描述(或者说二者互相表示).
从神经元和神经层的角度来看, 在第$l$ 层每个神经元$j$, 都有一个与上一层神经元$i$ 连接的权重$w_{ij}^{(l)}$, 以及每个神经元的偏置项$b^{(l)}_j$, 把权重矩阵记作$W^{(l)}$, 上一层$l-1$ 的输出$Y^{(l-1)}$ 给进当前层$l$ 记作本层输入$X^{(l-1)}$, 偏置向量记为$b^{(l)}$, 那么该层的输出$Y^{(l)}$ 为:
$$
Y^{(l)} = W^{(l)}X^{(l-1)} +b^{(l)}
$$
它的形式上就是单纯的线性回归. 如果只是这样, 神经网络不论有多少层, 输入输出都是线性的, 加不加隐藏层都一样, 是无法拟合非线性关系的. 这时候必须加入一些非线性元素使得神经网络具有非线性拟合的能力, 必须用某种方式给神经网络注入灵魂.
激活函数 Activation Function
激活函数是作用在神经元输出上的非线性函数, 最开始是被单独作为一个神经层而存在的, 后来被集成到神经元身上. 它使得神经网络具有了逼近任意函数的潜力, 只要神经元够多, 数据足够健壮, 那么它可以拟合任意的情况. 激活函数常用的只有几种, 现在最常见的是Relu, 解决了梯度爆炸和梯度消失的难题(后面提到). 在有了激活函数$f(x)$后, 每个神经元的输出变为了:
$$
Y^{(l)} = f(W^{(l)}X^{(l-1)} + b^{(l)})
$$
Sigmoid
它是早期很常见的激活函数, 但是因为存在一些缺陷, 近些年使用的人数越来越少. 公式如下:
$$
\sigma(x) = \frac{1}{1+e^{-x}}
$$
这个函数的导数很好求. 并且它能够将任意的输入都放缩到$[0, 1]$的区间内.
$$
\sigma’(x) = \sigma(x)(1-f(x))
$$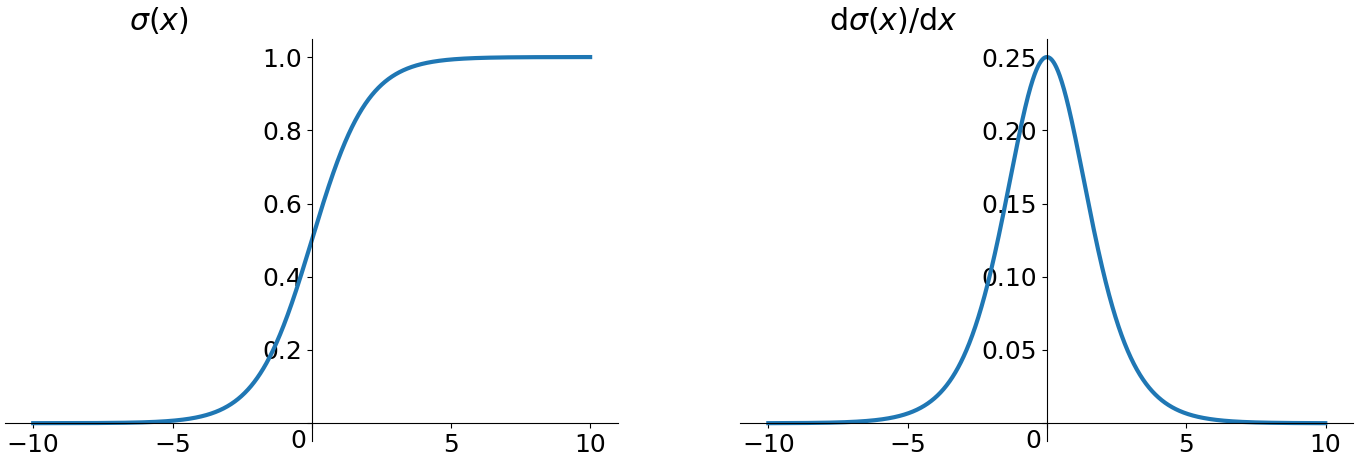
它的缺点也很明显, 当输入过大或过小时, 所对应的的导数近乎为0, 这种现象称为梯度消失. 这对于之后梯度下降的链式求导是极为不利的. 因为我们对神经网络的权值初始化范围在$[0, 1]$之间, 当发生反向传播时, 如果隐藏层特别多, 就很容易发生梯度消失, 使链式求导趋于0. 还有一个问题就是, Sigmoid每次输出的数据都不是Zero-centered, 其输出值全是正数, 会在收敛的路上越走越远, 导致收敛慢.
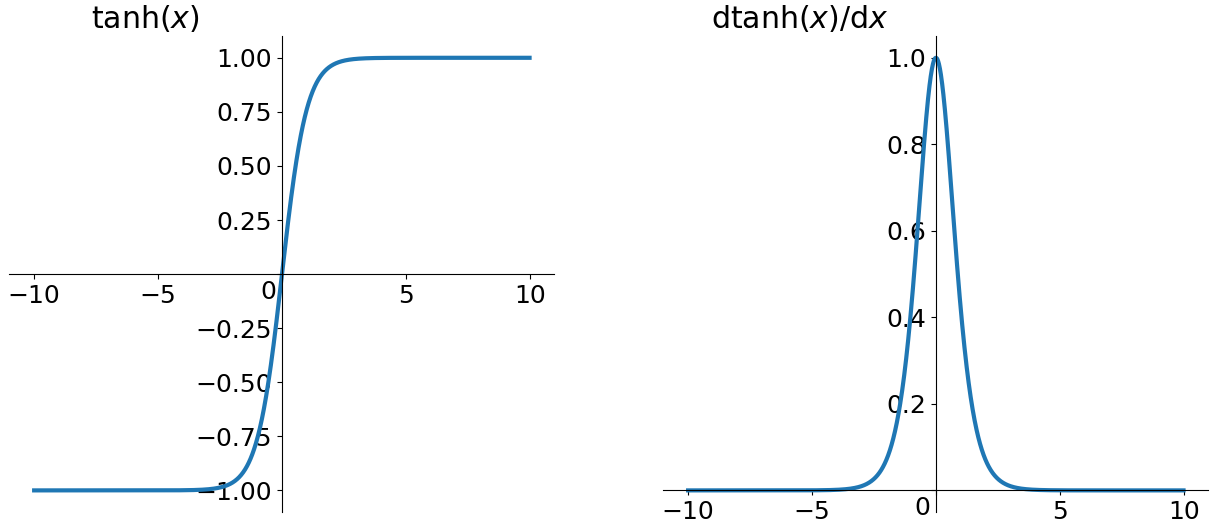
Tanh
Tanh不是很了解, 但是现在用在NLP里很多(RNN经常用).
$$
tanh(x) =\frac{e^x-e^{-x}}{e^x+e^{-x}} \
tanh’(x) = 1-tanh^2(x)
$$
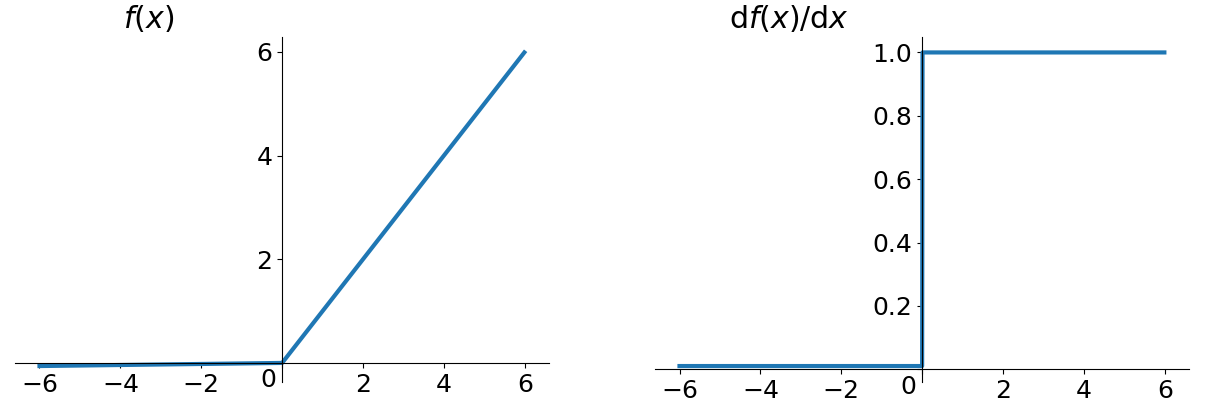
Relu
为了改善梯度消失和梯度爆炸的问题, 计算也非常简单. 当时的Relu是非常具有统治力的(现在也是).
$$
ReLu(x) = max(0, x)
$$
其实就是一个取最大值的函数, 如果输入是负数直接取0. 不是全区间可导, 但是可以取次梯度.
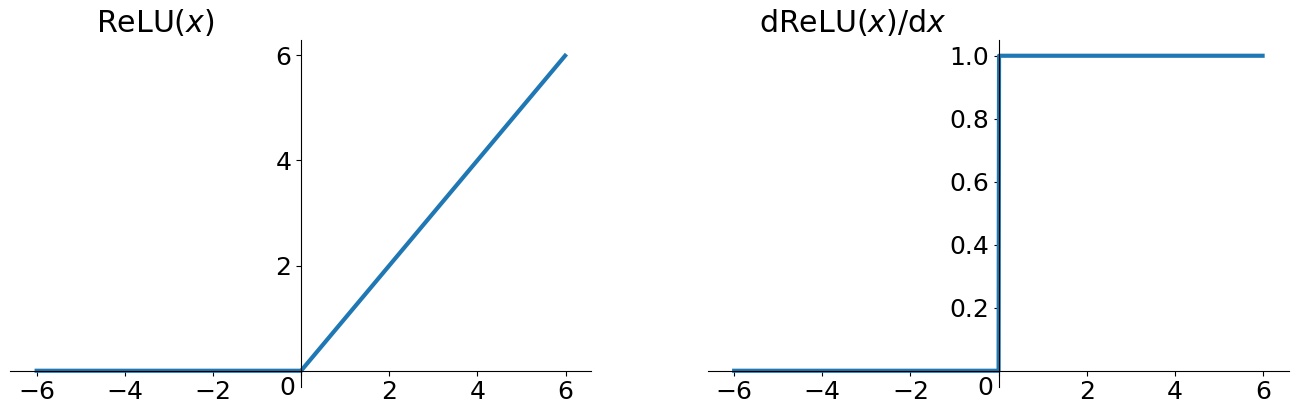
它的优点就是收敛快, 在输入大于0的情况下, 导数恒为1, 改善了梯度消失问题. 但是Relu的输出同样不是Zero-centered. 而且还有可能会造成Dead neuron. 因为有些输入是小于0的, 或者有些节点因为不幸的初始化或者Learning rate设的太大, 导致整个权重矩阵的分布发生变化, 若矩阵分布中心在负区域, 则负输入的梯度为0, 导致神经元可能永远不被更新.
基于这个问题, 人们提出了许多别的解决方案, 都是在负输入上做一些手脚. 比如说LeakyRelu, 在负输入区域上的值就不全为零, 而是用一个可以调整的参数$\alpha$(通常取0.01)乘上输入.即:
$$
LeakyReLu(x)=max(\alpha x, x)
$$
参数$\alpha$可以通过反向传播学习到. 理论上来说LeakyRelu会继承Relu的所有优点, 并改善它的缺点. 但是实际上并没有相关实验证明它会在所有情况下比Relu好.
Softmax
在处理多分类问题时, 最后一层上会使用Softmax函数作为激活函数. Softmax保证了最后神经元输出是以概率形式输出. 对于分$C$类的问题, 最后一层第$i$个神经元在未激活的情况下的输出$y_i$, 有:
$$
Softmax(y_i) = \frac{e^i}{\sum\limits_i^Ce^i}
$$
反向传播BP Back Propagation
深度神经网络也被称为BP神经网络, 就是指的反向传播. 反向传播可以说是神经网络中最重要的部分之一了. 这种方式告诉我们如何调整神经元的相关权重. 首先, BP是基于梯度下降来调整权重的. 对于第$l$层, 第$i$个神经元对下一层第$j$个神经的权重$w_{ij}$, 损失函数为$E$, 人为设定学习率$\eta$ , 更新$w_{ij}$有:
$$
w^{(l)}_{ij} = w^{(l)}_{ij} - \eta\frac{\partial E(W, b)}{\partial w^{(l)}_{ij}}
$$
对于每层的偏置$b^{(l)}$ 同理. 这其中涉及到链式求导, 因为在计算时, 是通过输出层的最终复合函数逐渐向输入层求导, 所以就叫反向传播.
随机失活 Dropout
当某些神经元过于强势时, 导致其他某些神经元会不被得到训练, 从而增大过拟合的几率, 当强大神经元对应输入的部分数据出现问题时, 就会出现单点故障. 所以需要一个方法使得其他神经元也得到训练, 并避免某些神经元过于强大. 此时, 采用神经元的随机失活策略, 使得每个神经元在训练时都有一定的概率权重不被更新, 能够保证绝大多数的神经元都处于活跃状态.
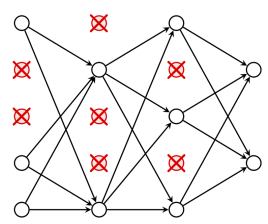
参数计算
DNN的参数计算比较简单, 假设第$l$层有$m$个神经元, 第$l+1$层有$n$个神经元, 那么$l$层的每个神经元都对应$l+1$层的$n$个权重, 外加一个偏置$b$, 第$l$层需训练的参数个数是$m\times n + 1$.

