本文前置知识:
DiffSinger: Singing Voice Synthesis via Shallow Diffusion Mechanism
本文是论文DiffSinger: Singing Voice Synthesis via Shallow Diffusion Mechanism 的阅读笔记和个人理解. 论文来自AAAI 2022.
主要是将DDPM应用于歌声合成, 做梅尔谱(Mel - Spectrogram)的生成. 需要有DDPM基础后在阅读.
Naive Version of DiffSinger
一个朴素的版本的DiffSinger就是将DDPM 直接应用于梅尔谱的生成:
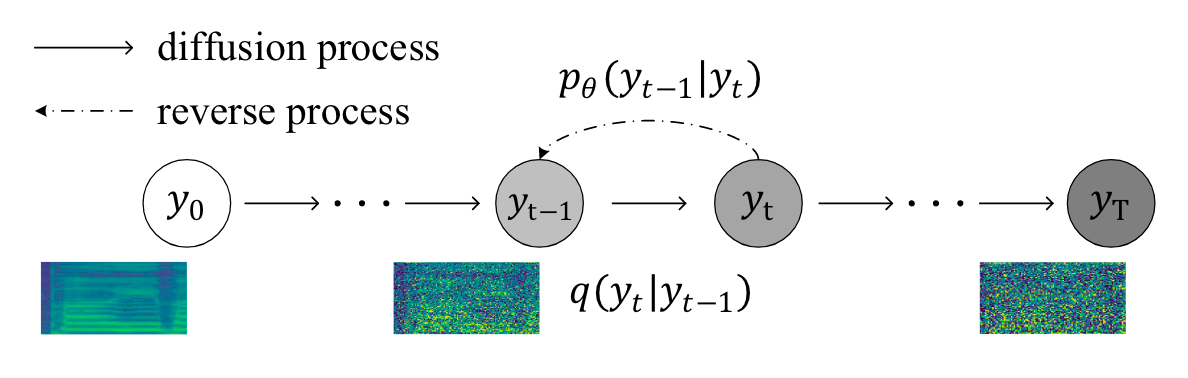
在训练阶段, DiffSinger直接将第$t$ 时刻的梅尔谱$M_t$ 用于去噪训练, 由Denoiser在Music Score $x$ 和时间步$t$ 的约束下预测随机噪声$\boldsymbol{\epsilon}_\theta (\cdot)$. 推理阶段, 直接标准正态分布的高斯噪声通过$T$ 次Reverse Process得到最终的梅尔谱$M_0$. Reverse Process描述与DDPM保持一致:
$$
M_{t-1}=\frac{1}{\sqrt{\alpha_t}}\left(M_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(M_t, x, t\right)\right)+\sigma_t \mathbf{z}
$$
其中$\mathbf{z} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$, 且当$t=1$ 时 $z = 0$.
Shallow Diffusion Mechanism
作者观察到歌声合成中目前现存的问题:
真实的梅尔谱$M$ 中往往蕴含着大量的细节, 可以运用于直接生成歌声. 然而现有的模型生成的梅尔谱往往具有过度平滑问题, 导致合成的歌声不够自然.
因此, 作者提出了一种浅扩散机制(Shallow Diffusion Mechanism), 来加速Diffusion Model在歌声合成上的性能和效率:
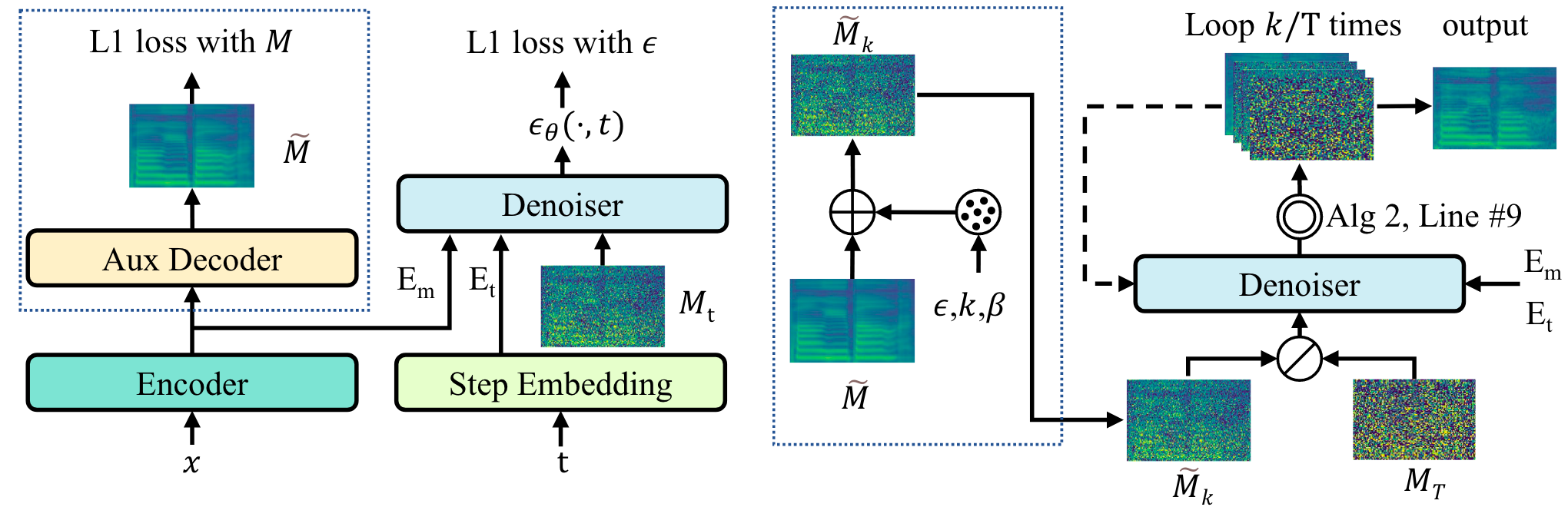
$\widetilde{M}$ 为一个以Music Score作为输入且用L1 Loss训练的Decoder预测出的梅尔谱, 虽然包含一部分歌声的有效信息, 但是梅尔谱上缺少细节, 存在模糊 / 过平滑问题.
作者观察到, 当$t \rightarrow T$ 时, $M, \widetilde{M}$ 都退化为正态分布的高斯噪声, 即$M_T, \widetilde{M}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$. 由于$\widetilde{M}$ 是$M$ 的过平滑版本, 如果$T$ 足够大, 在二者逐渐去噪得到梅尔谱的过程中, 应有一步$t=k$ 能使得$\widetilde{M}_k$ 近似于$M_k$.
即二者在迹上存在近似于$M_k$ 的交点$\widetilde{M}_k$:
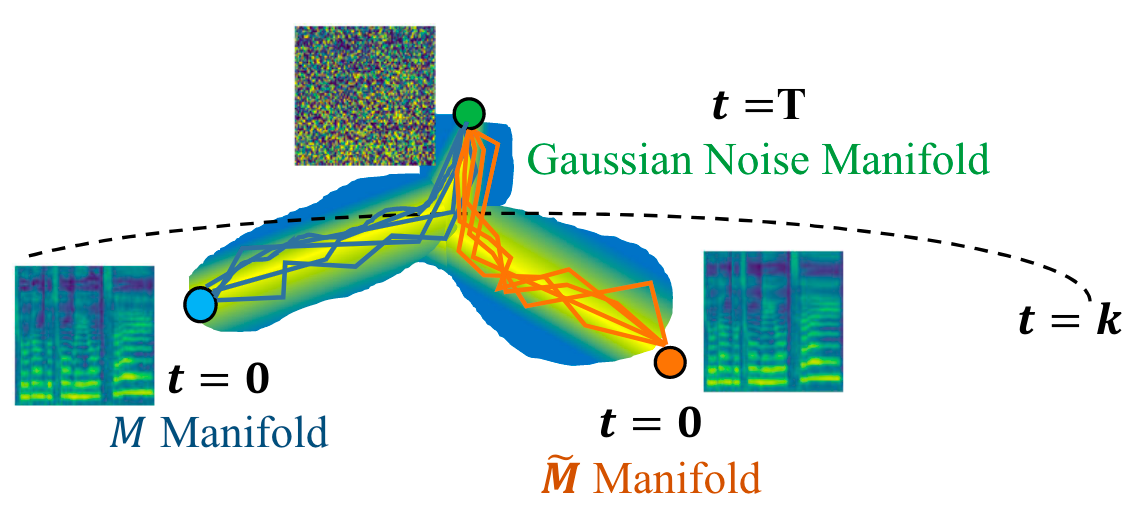
当$k$ 合适地被选择时, 可以认为$\widetilde{M}_k$ 和$M_k$ 来自于相同的分布, 从而可以直接从$\widetilde{M}_k$ 开始Reverse Process.
由于得到$\widetilde{M}_k$ 是计算量相对小且容易的, 并且$M_k$ 退回到$M_0$ 是比$M_T$ 退回到$M_0$ 简单的多的, 所以$\widetilde{M}_k$ 就可以直接代替$M_k$ 作为Reverse Process的起点.
$\widetilde{M}_k$ 可以直接由$\widetilde{M}$ 与噪声$\boldsymbol{\epsilon}$ 线性组合得到:
$$
\widetilde{M}_k(\widetilde{M}, \boldsymbol{\epsilon})=\sqrt{\bar{\alpha}_k} \widetilde{M}+\sqrt{1-\bar{\alpha}_k} \boldsymbol{\epsilon}
$$
其中, $\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}), \bar{\alpha}_k:=\prod_{s=1}^k \alpha_s, \alpha_k:=1-\beta_k$.
Boundary Prediction
作者设计了Boundary Predictor(BP)来确定$M, \widetilde{M}$ 之间的交点和$k$.
当然, $k$ 也可以作为超参手动搜出来.
BP实际上是一个Discriminator. 因为它的训练目标是区分输入的梅尔谱是来自于加噪后的真实梅尔谱$M_t$ 还是加噪后的Decoder合成的梅尔谱$\widetilde{M}_t$.
当梅尔谱来自于真实梅尔谱$M_t$ 时标签为1, 来自于Decoder生成的梅尔谱$\widetilde{M}_t$ 时记为0.
用BCE来优化Boundary Predictor:
$$
\mathbb{L}_{B P}=-\mathbb{E}_{M \in \mathcal{Y}, t \in[0, T]}\left[\log B P\left(M_t, t\right)+\log \left(1-B P\left(\widetilde{M}_t, t\right)\right)\right]
$$
$\mathcal{Y}$ 为训练集中的梅尔谱.
作者发现, 对于所有的$M \in \mathcal{Y}$, 有一早期Step $k^\prime$ 能使得位于$\left[k^\prime, T\right]$ 中几乎有95%的Time Step $t$ 都满足$\text{BP}\left(M_t, t\right)$ 和$\text{BP}\left(\widetilde{M}_t, t\right)$ 之间的距离都低于阈值. 此时可以选择$k^\prime$ 的平均值作为交点边界$k$.
Model Structure

- Encoder: 将Music Score转换为序列$E_m$.
- Lyrics Encoder: 编码Phoneme ID, 由Transformer Block堆叠组成, 最后获得Linguistic Embedding Sequence.
- Length Regulator: 用Duration Information将Linguistic Sequence扩展到梅尔谱长度.
- Pitch Encoder: 编码Pitch ID, 获得Pitch Sequence.
- 最后将Phoneme Sequence和Pitch Sequence相加.
- Step Embedding: 由正余弦位置编码和两层线性层获得时间步$t$ 时Channel为$C$ 的Step Embedding $E_t$.
- Auxiliary Decoder: 简单的梅尔谱生成器, 用堆叠的Transformer Block组成, 与FastSpeech2结构相同, 获得合成的梅尔谱$\widetilde{M}$.
- Denoiser: 采用Non - causal的WaveNet结构. Denoiser $\boldsymbol{\epsilon}_\theta$ 在给定Step Embedding $E_t$ 和Music Condition $E_m$ 的条件下预测梅尔谱$M_t$ 的噪声$\boldsymbol{\epsilon}$.
- Boundary Predictor: ResNet和5层堆叠的CNN. 根据给定的$E_t$ 区分梅尔谱到底是来自于$M_t$ 还是$\widetilde{M}_t$.
Training & Inference
训练过程分为两个阶段:
- Warmup Stage: 分别训练Auxiliary Decoder + Music Score Encoder 160k steps, 然后再用Aux Decoder训Boundary Predictor 30k steps. 使得Aux Decoder具备一定的梅尔谱合成能力, 再根据Decoder训练BP.
- Main Stage: 训DiffSinger 160k steps直至收敛.
在获得了$M_t$ 与$\widetilde{M}_t$ 的交点边界$k$ 以后, DiffSinger的训练过程就是DDPM里的标准训练过程:

推理过程和DDPM相似, 只不过是令$\widetilde{M}_k$ 近似为$M_k$, 然后从$\widetilde{M}_k$ 开始Reverse Process:

推理过程中采用Parallel WaveGAN(PWG)作为Vocoder将梅尔谱合成为声波.
Experiments
详细的模型参数设置和实验设置请参考原论文.
Main Results and Analysis
Audio Performance
为了评价DiffSinger在感知上DB表现, 首先进行了MOS(Mean Opinion Score)评估. 让18个Listener根据主观评价它们对测试集歌声合成的听感打分, 结果如下:
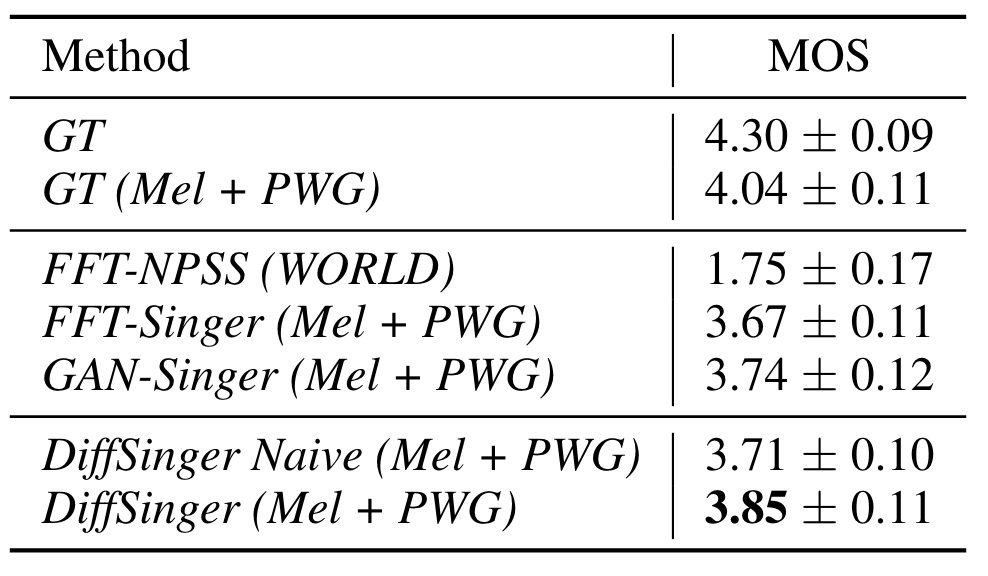
GT(Mel + PWG)可以视为是SVS模型的性能上限. DiffSinger表现要优于基于GAN和FFT(Feed Forward Transformer).

DiffSinger(b) 相对于GAN(c)和FFT(d) 来说, 过平滑问题缓解了许多, DiffSinger能生成更多的细节, 总体表现于GT(a)更相似. (c, d) 中的过平滑问题比较明显.
Ablation Studies
接着进行了超参搜索的消融实验.
$T$ 统一设置为100, $C$ 为Channel Size, $L$ 为Denoiser的层数, 结果如下:
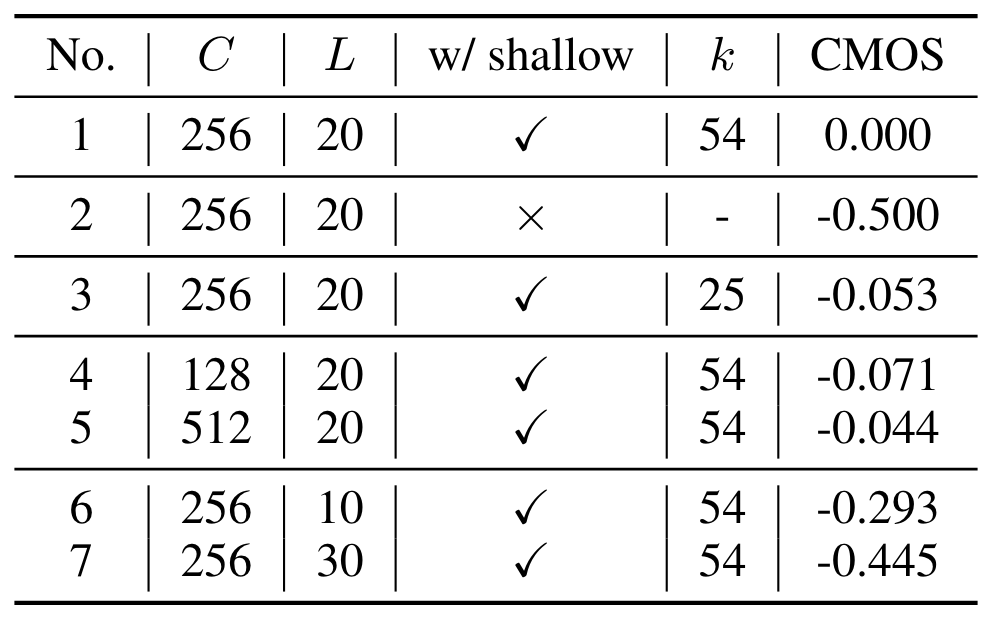
三个结论:
- 性能变化最大的是使用 / 不使用 Shallow Diffusion, 结果相差了0.5CMOS.
- 在选择了一个不是Boundary Predictor预测出的$k$ 时, 性能发生退化, 说明Boundary Predictor是有作用的.
- 当$L$ 为10, 30时方法性能退化比较大, 作者的解释是DiffSinger模型容量充分.
看样子BP的作用甚至都没有$L$ 的影响大… 可以考虑进一步对比在$k$ 为25时$L$ 为10和30的表现进一步说明BP的作用.
Extensional Experiments on TTS
最后, 作者在TTS上进行了实验说明DiffSinger方法的泛用性, 称为DiffSpeech:
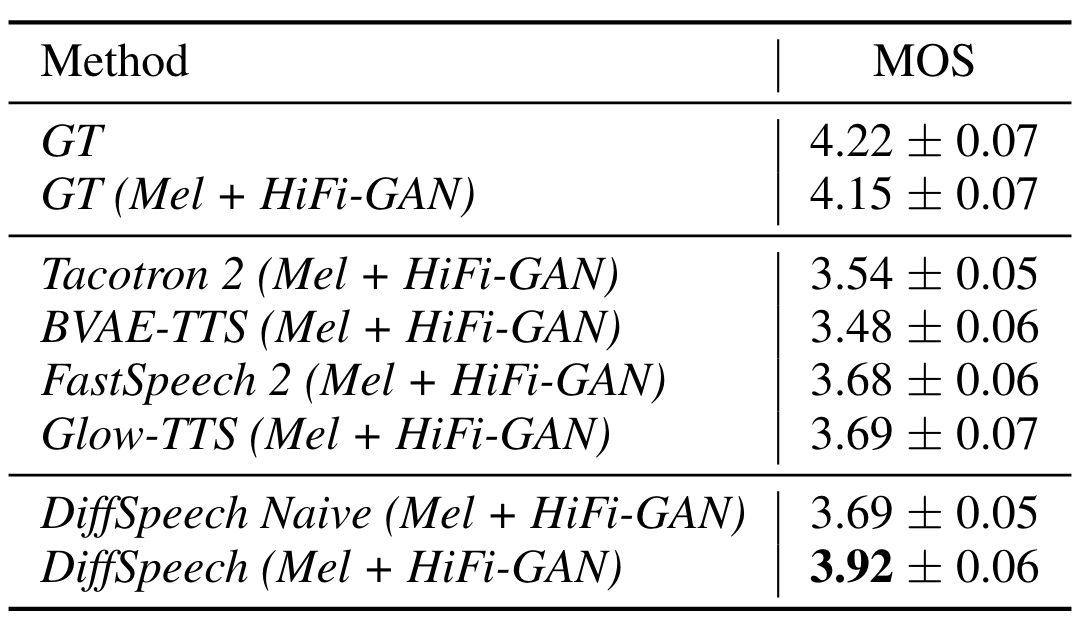
DiffSpeech Naive的表现和Glow - TTS / FastSpeech2接近.
在采用了Shallow Diffusion以后, DiffSpeech的表现相较于其他TTS方法有了大幅提升, 并且获得了29.2%的加速.
Summary
我第一回了解到DiffSinger是在B站刷到这首歌, 并留下了非常深刻的印象.
DiffSinger作为具有代表性的将Diffusion应用于SVS的方法, 已经在B站产生了一定影响力, Github上也有OpenVPI 维护的版本.
总的来说, 作者比较巧妙的结合现有模型在梅尔谱生成上的缺陷, 将梅尔谱生成拆分成梅尔谱的大致形态的生成(Auxiliary Decoder)和梅尔谱细节(Diffusion)生成的两部分. 缓解了SVS中的过平滑问题.

