发布日期: 2022-04-02

更新日期: 2024-06-29

文章字数: 10.9k

阅读时长: 45 分

2022.04.14: AlphaGo施工完成.

Introduction: Deep Reinforcement Learning

本文介绍的是Deep Reinforcement Learning(深度强化学习)入门相关知识, 适合想要入门理解或者直接使用DRL的读者. 文中包含有大量的公式, 在学习DRL时是根本逃避不开的, 如果哪里卡壳了可以去Recommended中找找有没有相关内容.

大多数内容来自【王树森】深度强化学习(DRL), 我觉得是非常棒的课程. 虽然贴的链接是B站的, 转载油管上的视频, 但是评论区里附有视频内容节点.

文中所涉及的所有图片出处在结尾都会提供.

Terminology

Reinforcement Learning(RL)旨在通过智能体与环境的不断交互, 教会智能体如何执行任务, 比如让人工智障自己学会玩超级玛丽.

RL相关的术语很多, 下面先在超级玛丽这一游戏场景下介绍RL里面的相关概念.

Agent(智能体): 强化学习的主体. 即玛丽奥.
State(状态): 环境的状态, 记为$s \in \mathcal{S}$, 可以理解成超级玛丽的游戏画面.
Action(动作): 智能体基于当前环境状态可以做出的行为. 记为$a \in \mathcal{A}$. 例如玛丽奥可以向上, 左右跑动.

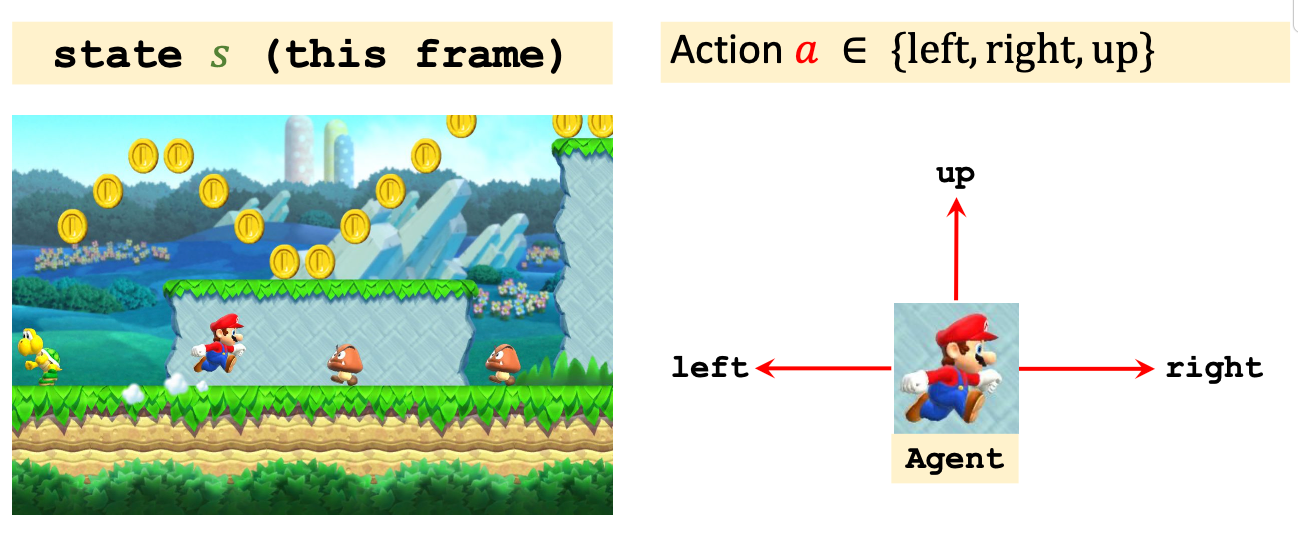
Policy(策略): Agent应该根据状态做出什么决策, 其数学描述是个概率密度函数(在这里说的不严谨, 因为例子是一个离散的):
$$
\pi(a \mid s)=\mathbb{P}(A=a \mid S=s)
$$
根据给出的状态$s$, 都能根据$\pi(a\mid s)$给出一个做出动作$a$ 的概率. 例如在当前超级玛丽画面下, 策略函数可以判断出玛丽奥应该向上走, 还是向左向右走.
为什么要让策略$\pi$ 是随机的? 我认为有两个原因:
1. 因为在与环境的交互中, 如果Agent一直保持恒定的策略运作, 很大概率会被不断变化的环境所击垮. 在后面也可以发现, 在强化学习中, Agent和环境始终保持博弈, 所以才要让Agent的策略变化多端.
2. 鼓励Agent做一些随机动作, 不断探索做出不同动作对环境的影响. 尤其是在Agent训练早期, 随机性应该设置的更大一些.

Reward(奖励): Agent做出动作后, 给予Agent的奖励, 记为$R$. 其定义方法不唯一. 例如打赢超级玛丽可以定义非常多的奖励, 而吃金币只能获得少量奖励, 被打死要给予负的奖励.
State Transition(状态转移): 环境因Agent做出了某个动作后从旧状态变为新状态的过程. 可以是确定的也可以是, 通常认为是随机的, 状态转移的随机性来自于环境. 例如玛丽奥的敌人可能向左走也可能向右走. 同样可以用概率密度函数来表示:
$$
p(s^\prime\mid s, a) = \mathbb{P}(S^\prime=s \mid S=s, A=a)
$$
状态转移函数仅有环境自己可知.
Episode: RL里的epoch不叫epoch, 与之类似的概念叫 episodes, 指智能体从游戏开始到通关或者结束的过程, 也就是玛丽奥直至通关或死亡的过程称为一个Episode. 因为RL对样本数量要求非常高, 所以让Agent玩一个游戏可能需要成千上万把.

Randomness in Reinforcement Learning

在RL中, 存在两种随机性,

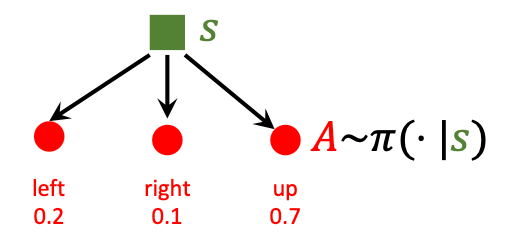
Actions have randomness: Policy函数根据State选择动作的时候存在随机性, 动作是根据Policy Function抽样得到的. 它是Agent的随机性.
State transitions have randomness: 状态转移存在随机性, 系统的状态转移也是根据抽样得来的. 它是Environment的随机性.

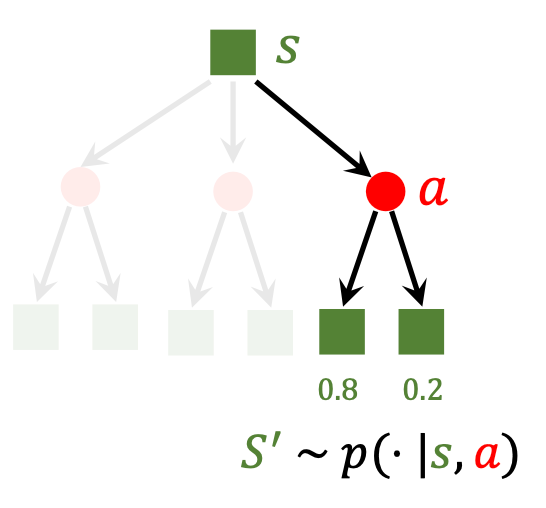
本节虽然简短, 但对后续理解Return和Value Function的概念至关重要.

Agent - Environment Interaction

下面描述一下Agent和Environment的交互过程:

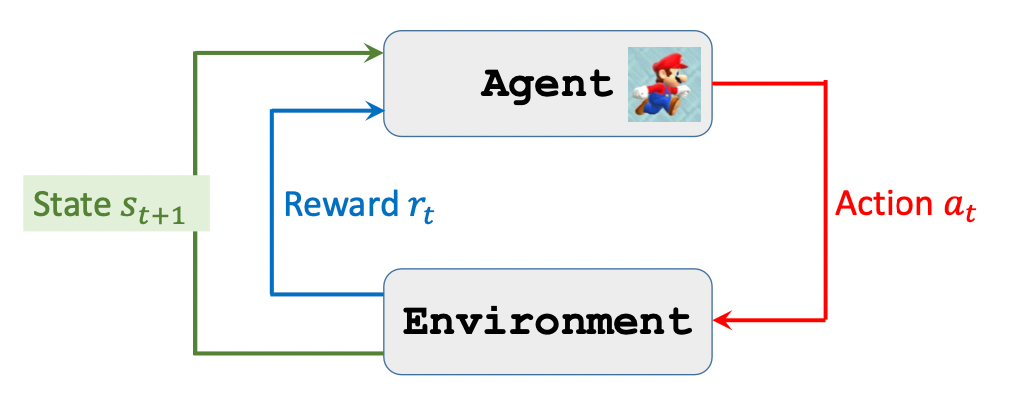
Agent总是和环境循环的按照下面的流程交互:

观察环境, 得到状态$s_1$.
Agent做出动作$a_1$.
环境状态转移, 得到状态$s_2$, 同时给予Agent奖励$r_1$.
Agent做出动作$a_2$.
……

它对应着这样一幅图:

由此我们可以得到一组关于(state, action, reaward)的Trajectory(迹):
$$
s_1, a_1,r_1,\ s_2, a_2, r_2,\ \cdots,\ s_T, a_T, r_T.
$$
$T$ 为结束时刻.

Rewards and Returns

Return

Return(回报)指的是当前时刻开始到这个episode结束时奖励的和, 它的另一个名字是Cumulative Future Reward(未来累计奖励), 所以它和当前时刻的奖励$R_t$ 不是同一个概念:
$$
U_t= R_t+ R_{t+1} + R_{t+2} + R_{t+3} + \cdots
$$
在RL中认为, 对于Agent来说, $R_t$ 比$R_{t+1}$ 要更重要, 即未来的奖励没有现在的奖励重要, 因为未来的不确定性更大, 同样都是奖励, 不如立刻得到奖励 ,而非. 这就引出了另一个概念, Discounted Return(折扣奖励, 也叫折扣未来累计奖励):
$$
U_t= R_t+ \gamma R_{t+1} + \gamma^2 R_{t+2} + \gamma^3 R_{t+3} + \cdots
$$
$\gamma \in [0, 1]$, 叫折扣率, 是个超参. 如果未来和现在的奖励权重相同, 那就令$\gamma=1$, 如果根本不考虑未来的奖励, 那就令$\gamma=0$.

一般情况下, RL中说Return指的都是Discounted Return.

为什么要定义Return呢? 因为RL的目标是最大化Return, 而非最大化Reward. 下棋时我们应该赢得整个比赛(Return), 而不是吃掉对面一个棋子(Reward).

Randomness in Returns

在任意时刻$t$, Return $U_t$ 是随机的. 因为Return由未来的Reward构成, 而未来时刻$i \geq t$ 的Reward $R_i $ 由Action $A_i$ 和State $S_i$决定, 但Action和State是随机的, 所以Return也是随机的.

观测值不具有随机性(小写字母), 未知的随机变量有随机性(大写字母).

同时注意到, Return依赖于未来. 根据$U_t$ 的定义, 对于已观测到的$s_t$, $U_t$ 由随机变量$A_t, A_{t+1}, A_{t+2}, \cdots$ 以及$S_{t+1}, S_{t+2}, \cdots$ 决定.

Value Functions

Action - Value Function

前面说过Return依赖于未来, 在当前时刻$t$, 未来的Return是随机变量, 然而我们根本不可能预知未来, 不可能在$t$ 时刻直接知道$U_t$ 是什么, 因为我们不知道未来的Reward是多少. 我们在抛硬币之前并不知道抛出去的硬币是正面还是反面.

那我们如何评估当前形式? 因为$U_t$ 是个随机变量, 那我们就把所有的随机性全都积掉(也就是求期望). 虽然在抛硬币之前不知道会抛出正面还是反面, 但应该知道正反面各有一半的概率, 并且当正面记作1, 反面记作0时可得到期望0.5.

$U_t$ 取决于$A_t, A_{t+1}, A_{t+2}, \cdots$ 和$S_{t+1}, S_{t+2}, \cdots$, 从$t+1$ 时刻起的所有动作和状态都具有随机性, 如果把$U_t$ 视为$s_t$ 和$a_t$ 的函数, 求条件期望可以去掉随机, 这个函数被称为Action - Value Function(动作价值函数):
$$
Q_{\pi}\left(s_{t}, a_{t}\right)=\mathbb{E}\left[U_{t} \mid S_{t}=s_{t}, A_{t}=a_{t}\right]
$$

动作的概率密度函数是策略函数 $\mathbb{P}(A=a \mid S=s) = \pi(a \mid s)$.
状态的概率密度函数是状态转移函数 $\mathbb{P}(S^\prime=s \mid S=s, A=a) = p(s^\prime\mid s, a)$.
动作价值函数与$\pi$ 有关. 因为在不同策略函数$\pi$ 下, 条件期望不同.

它更准确地说应该叫动作状态价值函数, 因为它依赖$s_t, a_t$ 两个变量. 但大家习惯的称之为动作价值函数.

除了已观测到的$s_t$ 和$a_t$, 其余的未来随机变量$A_{t+1}, A_{t+2}, \cdots$ 和$S_{t+1}, S_{t+2}, \cdots$ 都被积掉了.

动作价值函数直观的告诉我们, 如果用策略函数$\pi$, 在$s_t$ 下做$a_t$ 是好还是不好, 就可以根据当前局势对动作打分.

因为动作价值函数跟$\pi$ 有关, 想要把$\pi$ 去掉只需要令Agent找到使得$Q_\pi$ 最大化的那种策略, 即Optimal Action - Value Function(最优动作价值函数):
$$
Q^{\star}\left(s_{t}, a_{t}\right)=\max _{\pi} Q_{\pi}\left(s_{t}, a_{t}\right)
$$
得到了最优动作价值函数$Q^\star$ 后, Agent直接根据$Q^\star (s_t, A)$ 的值就能直接做出决策.

State - Value Function

如果Agent想知道当前状态 / 局势$s_t$ 对自己好不好, 就得在动作价值函数的基础上把$A$ 也给积掉, 或者说无论Agent做出什么动作, 环境状态对Agent来说如何?

这就引出了State - Value Function(状态价值函数)的概念. 假如$A$ 是离散的,
$$
V_{\pi}\left(s_{t}\right) =\mathbb{E}_A\left[Q_{\pi}\left(s_{t}, A\right)\right]
=\sum_{a \in \mathcal{A}} \pi\left(a \mid s_{t}\right) \cdot Q_{\pi}\left(s_{t}, a\right)
$$
如果$A$ 是连续的就求积分:
$$
V_{\pi}\left(s_{t}\right) =\mathbb{E}_A\left[Q_{\pi}\left(s_{t}, A\right)\right]
=\int_{a \in \mathcal{A}} \pi\left(a \mid s_{t}\right) \cdot Q_{\pi}\left(s_{t}, a\right)\mathrm{d}a
$$

$V_\pi$ 还能评价$\pi$ 的好坏, 如果$\pi$ 越好, 去掉状态的不确定性(对$S$ 求期望)后的值$\mathbb{E}_S\left[V_{\pi}\left(S\right)\right]$ 就越大.

Value - Based Reinforcement Learning

请理解并回顾价值函数相关概念.

假设$Q^\star$ 已知, Agent直接变身预言家, 直接根据$Q^\star$ 判断在$s$ 下什么才是最优的动作, 即$a^{\star}=\underset{a}{\operatorname{argmax}} Q^{\star}(s, a) $, 然而$Q^\star$ 未知, Agent并不能变身预言家. Value - Based RL思想就是通过某种方法近似出$Q^\star$.

Deep Q - Network

Agent不能变身预言家, 除非… 除非Agent玩了无数把超级玛丽, 对超级玛丽, 那它也和先知没什么区别了, 瞅一眼屏幕就能告诉你要选什么Action.

行啊, 那我就玩呗. Deep Q - Network(DQN) 正是基于这个想法, 用神经网络$Q(s, a;\mathbf{w})$来近似$Q^\star(s, a)$, 即:
$$
Q(s, a, \mathbf{w}) \approx Q^\star (s, a)
$$

请注意, DQN近似的是最优动作价值函数$Q^\star(s, a)$, 而不是动作价值函数$Q_\pi(s, a)$.

举个例子, 让神经网络玩无数次超级玛丽, 用CNN来捕获屏幕上的State Feature, 然后喂给全连接层给出当前状态特征下不同动作的打分(离散Action):

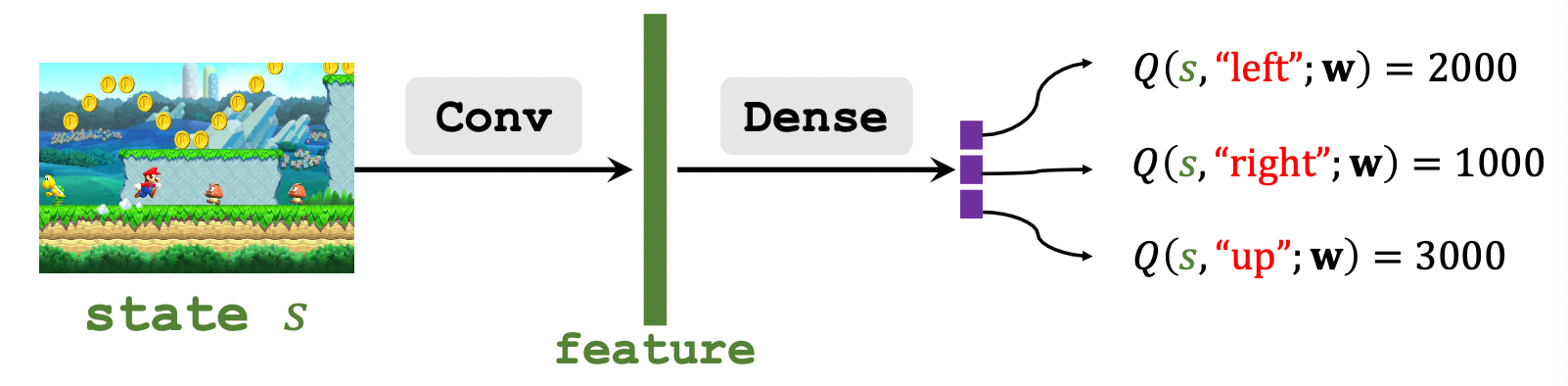
向上的$Q$ 最大, 所以让玛丽奥往上跳更好.

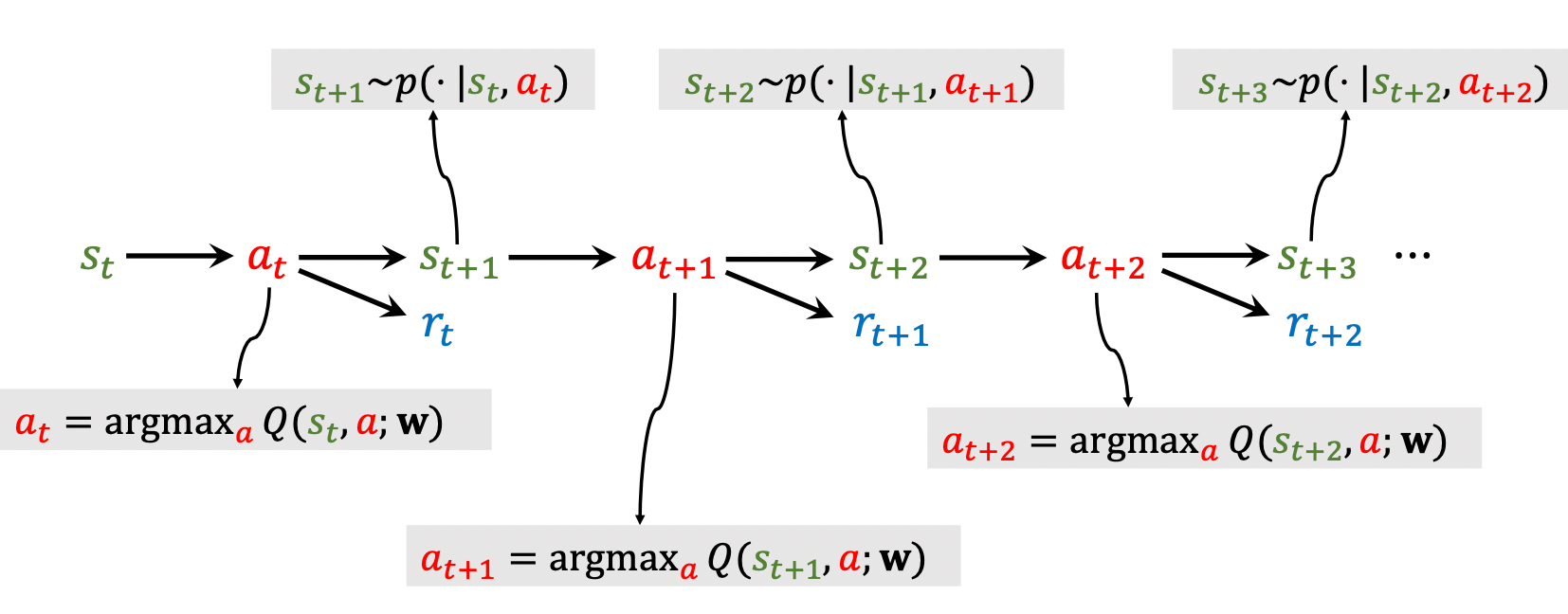
所以DQN的RL流程很简单嘛:

观察环境状态$s_t$, 比如用CNN来捕获特征.
用DQN获得Agent各个动作的打分, 让Agent做出打分最大的动作$a_t$.
环境根据$a_t$ 发生状态转移, 新状态为$s_{t+1}$, 同时给予Agent奖励$r_t$.
……

Temporal Difference (TD) Learning

Temporal Differnece(时间差分)算法是训练DQN最常用的方法.

Scenario

设想一个场景, 我们需要从NYC开车到Atlanta. 模型$Q(\mathbf{w})$给出了一个预估花费时间为1000mins, 我们走完全程后发现实际花费时间为860mins:

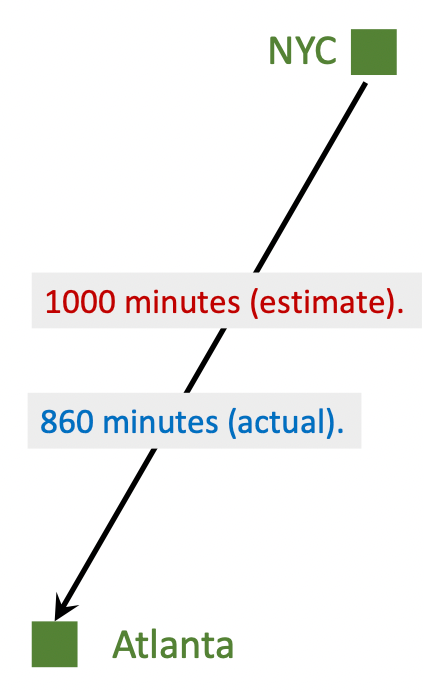
如何更新我们的模型? 很简单对吧, 只需要用均方误差作为Loss, 然后用梯度下降就行了:

$q=Q(\mathbf{w}), q=1000, y=860$.
Loss: $L = \frac{1}{2} (q-y)^2$.
Gradient: $\frac{\partial L}{\partial \mathbf{w}} = \frac{\partial{L}}{\partial{q}} \cdot \frac{\partial{q}}{\partial{\mathbf{w}}} = (q-y)\cdot \frac{\partial Q(\mathbf{w})}{\partial\mathbf{w}}$.
Gradient Descent: $\mathbf{w}_{t+1} = \mathbf{w}_t - \alpha \cdot \frac{\partial{L}}{\partial\mathbf{w}}|_{\mathbf{w}=\mathbf{w_t}}$.

但是这样太憨了, 我们从NYC到Atlanta的预测可能不那么靠谱, 因为这段测算距离太远了. 如果说我在旅途中发现NYC到DC用了300mins, 而此时模型测算从DC到Atlanta所需时间为600mins, 所以我根据新的模型估计, 此时需要的总共时间可能是900mins:

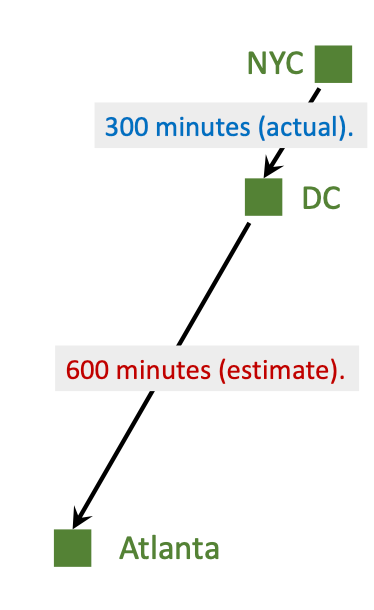
虽然900mins不一定是最终花费时间, 但是肯定比直接从NYC开始测算的1000mins靠谱得多. 900mins称为TD Target. 我们假设TD Target给出的900mins就是Ground Truth, 然后依然按照前面的方式更新模型参数:

$q=Q(\mathbf{w})=1000, y=300+600=900$.
Loss: $L = \frac{1}{2}{\left(Q\left(\mathbf{w}\right)-y\right)}^2$.
Gradient: $\frac{\partial L}{\partial\mathbf{w}} = \frac{\partial{L}}{\partial{q}} \cdot \frac{\partial{q}}{\partial{\mathbf{w}}} = \left(Q\left(\mathbf{w}\right)-y\right)\cdot \frac{\partial Q(\mathbf{w})}{\partial\mathbf{w}}=(1000-900)\cdot\frac{\partial Q(\mathbf{w})}{\partial\mathbf{w}}$.
Gradient Descent: $\mathbf{w}_{t+1} = \mathbf{w}_t - \alpha \cdot \frac{\partial{L}}{\partial\mathbf{w}}|_{\mathbf{w}=\mathbf{w_t}}$.

$Q(\mathbf{w}) -y = 1000-900=100$ 也称为TD Error $\delta$.

模型原来估计NYC到Atlanta用掉1000mins, DC到Atlanta用掉600mins, 按照模型估计, NYC到DC需要400mins, 但是到DC的时候发现实际只花了300mins, 比400mins要快:

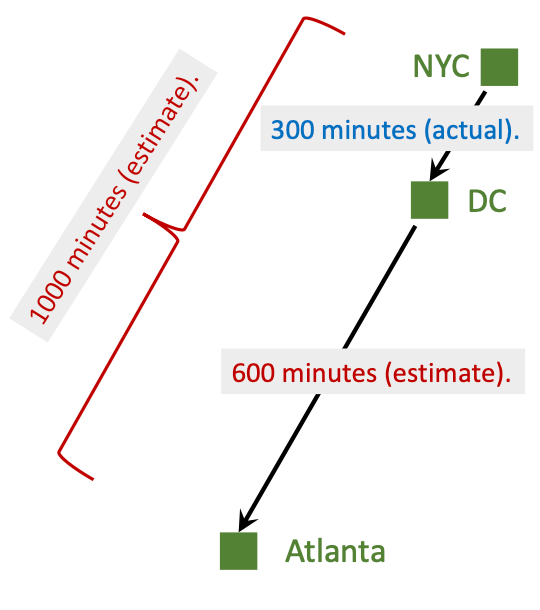
因此从NYC到DC这段旅途中, 模型估计的400mins和真实观测时间300mins的差就是TD Error, 与我们前面的计算值相同. 理想状态下我们肯定希望TD Error为0, 也就是模型估计和真实观测时间相同. TD算法的目的最小化TD Error, 来减小损失.

从DC到Atlanta的模型预测实际上是跟模型参数相关的$\mathbf{w}$ 的函数, 但TD算法在求解时常常忽略这一点, 把它当做常数.

为什么TD算法比模型原来一次测算靠谱呢? 因为TD算法中所利用的信息不单单是模型的预测, 包含了一定的事实依据. 当我们的位置越接近Atlanta, 可以利用的事实越多, 估计就越准确. 换个角度来说, 观测到的事实消除了模型预测时附加进去的未知性, 既定事实已经没有未知干扰, 所以TD更准.

TD Learning for DQN

把TD算法应用在DQN上是相同的道理, 我们在旅途中途就可以更新模型参数, 是因为它有这样一个关系存在:

模型的完整预测可以被拆分为已经观测到的事实和模型剩余预测.

非常巧的是, 在深度强化学习中也有一个类似的式子存在:
$$
Q\left(s_{t}, a_{t} ; \mathbf{w}\right) \approx r_{t}+\gamma \cdot Q\left(s_{t+1}, a_{t+1} ; \mathbf{w}\right)
$$
回想一下我们之前讲过的Discounted Return $U_t$ 的定义, 不难明白为什么也存在类似的关系.
$$
\begin{aligned}
U_t&= R_t+ \gamma R_{t+1} + \gamma^2 R_{t+2} + \gamma^3 R_{t+3} + \cdots \\
&= R_t+ \gamma \cdot \left(R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots \right) \\
& = R_t + \gamma \cdot U_{t+1}
\end{aligned}
$$
对上式两边同求个期望:
$$
\mathbb{E}\left[U_t\right] = \mathbb{E} \left[R_t + \gamma \cdot U_{t+1}\right]
$$
在DQN里面, 用神经网络来近似动作价值函数$Q$, 所以$Q(s_t, a_t; \mathbf{w})$ 是$U_t$ 的估计$\mathbb{E}[U_t]$, $Q(S_{t+1}, A_{t+1}, ; \mathbf{w})$ 是$U_{t+1}$ 的估计$\mathbb{E}[U_{t+1}]$. 因此就有:
$$
Q(s_t, a_t; \mathbf{w}) \approx \mathbb{E}\left[R_t + \gamma \cdot Q\left(S_{t+1}, A_{t+1}, ; \mathbf{w}\right)\right]
$$
所以我们这样训练DQN:

Prediction: $Q(s_t, a_t; \mathbf{w}_t)$.
TD Target:
在$t+1$ 时刻, 可以观测到奖励$r_t$ 和新的状态$s_{t+1}$, 新的动作$a_{t+1}$ 可以由$Q$ 得到, 故TD Target $y_t$:

$$
\begin{aligned}
y_t&= r_t + \gamma \cdot Q(s_{t+1}, a_{t+1} ; \mathbf{w}_t) \\
&= r_t + \gamma \cdot \underset{a}{\max}Q(s_{t+1}, a; \mathbf{w}_t)
\end{aligned}
$$

Loss: $L_t = \frac{1}{2}{[Q(s_t, a_t; \mathbf{w}) - y_t]}^2$.
Gradient Descent: $\mathbf{w}_{t+1} = \mathbf{w}_t - \alpha \cdot \frac{\partial{L_t} }{\partial\mathbf{w}} |_{\mathbf{w}=\mathbf{w}_t} $.

实际上这样并不好训练, 因为我们目前所说的DQN兼顾了输出左侧$Q(s_t, a_t; \mathbf{w})$ 和右侧$Q(s_{t+1}, a_{t+1} ; \mathbf{w}_t)$ 的任务, 反向传播的时候会把两个更新结果放在一起. 如果网络$Q(s, a;\mathbf{w})$ 被更新, 那么右侧的值也会发生变化, 导致训练时候不太稳定. 所以后面会有针对DQN更高阶的技巧.

Policy - Based Reinforcement Learning

请理解并回顾策略函数, 价值函数, 回报相关概念.

有了好的策略$\pi(a \mid s)$, 就能用$\pi$ 根据环境$s$ 自动控制Agent. 问题是如何得到好的策略$\pi^\star$.

Policy Network

如果状态$S$ 和动作$A$ 的数量比较少, 那策略$\pi(a \mid s)$ 直接画一张表, 穷举出所有的可能性不就好了. 但是超级玛丽这样的游戏有无数状态, 没法用一张表搞定, 所以我们就得用一种方法来近似.

"神经网络时代的哲学: 难算的我们都用神经网络来拟合!"

----苏剑林

我们用神经网络来近似策略函数$\pi(a|s)$, 这种神经网络称为Policy Network(策略网络), 记$\pi(a \mid s, \boldsymbol{\theta})$. 其中$\boldsymbol{\theta}$ 是网络可训练参数, 因为Policy Function给出的是选择各个Action的概率, 只要满足$\sum_{a\in \mathcal{A}}\pi(a \mid s; \boldsymbol{\theta})=1$ 即可.

拿超级玛丽来说, 可以把网络设计成这样:

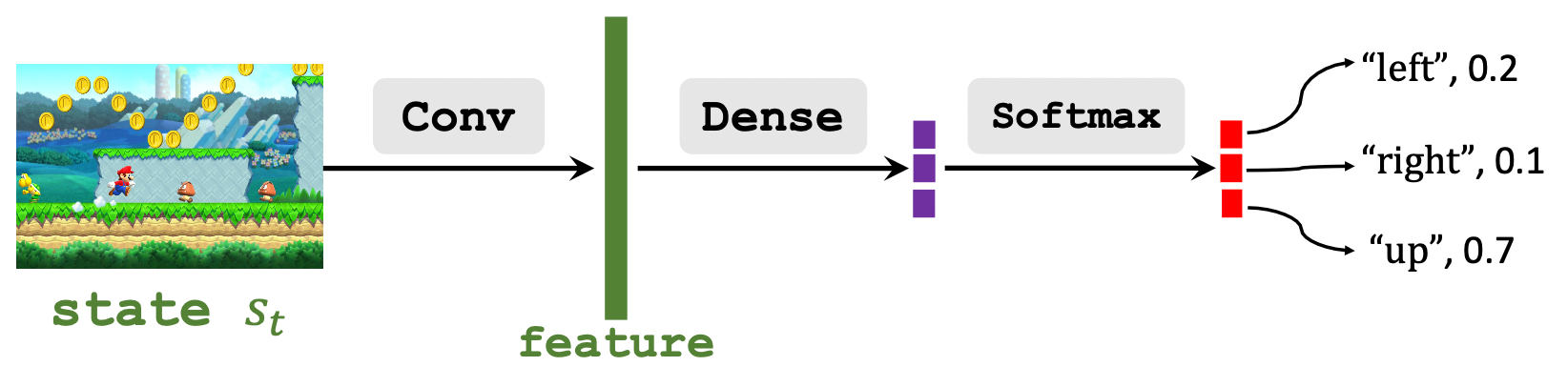
在超级玛丽中DQN和Policy Network区别不大对吗(仅仅在这个例子中)? 除了最后多加了一层Softmax.

State - Value Function Approximation

Policy - Based Reinforcement Learning

因为我们用的是策略网络$\pi\left(a \mid s_{t};\boldsymbol{\theta}\right)$, 而状态价值函数的计算是由策略函数推导来的, 所以状态价值函数也需要做相应的近似:
$$
\displaylines{
V_{\pi}\left(s_{t}\right) =\mathbb{E}_A\left[Q_{\pi}\left(s_{t}, A\right)\right]
=\sum_{a \in \mathcal{A}} \pi\left(a \mid s_{t}\right) \cdot Q_{\pi}\left(s_{t}, a\right) \\
\Downarrow \\
V\left(s_{t};\boldsymbol{\theta}\right)
=\sum_{a \in \mathcal{A}} \pi\left(a \mid s_{t};\boldsymbol{\theta}\right) \cdot Q_{\pi}\left(s_{t}, a\right)
}
$$
状态价值函数现在只和状态$s_t$, 策略网络模型参数$\boldsymbol{\theta}$ 有关, $V_\pi$ 中的$\pi$ 被整合到了$\boldsymbol{\theta}$ 当中.

策略网络$\pi(a\mid s;\boldsymbol{\theta})$ 越好, $V(s;\boldsymbol{\theta})$ 的值就越大. 通过改进模型参数最大化$V$ 就能使得模型参数$\boldsymbol{\theta}$ 越来越好, 这是策略学习最核心的思想. 基于这个想法, 可以写出策略学习的目标函数:
$$
J(\boldsymbol{\theta})=\mathbb{E}_{S}[V(S ; \boldsymbol{\theta})]
$$
求期望后只和$\boldsymbol{\theta}$ 有关, 与状态$S$ 无关. 我们可以放心的优化模型参数了.

实际求的时候不可能真正去求期望, 一般是随机采样得到.

如果观测到状态$s$, 用Policy Gradient ascent(策略梯度上升)来优化$\boldsymbol{\theta}$:
$$
\boldsymbol{\theta} \leftarrow \boldsymbol{\theta}+\beta \cdot \frac{\partial V(s ; \boldsymbol{\theta})}{\partial\boldsymbol{\theta}}
$$
$\beta$ 为学习率. 但这里的梯度指的是策略梯度.

Policy Gradient

本小节中, 将涉及到如何推导和近似求解策略梯度. 可以选择性阅读.

不严谨的推导Policy Gradient:
$$
\begin{aligned}
\frac{\partial V(s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} &=\frac{\partial \sum_{a} \pi(a \mid s ; \boldsymbol{\theta}) \cdot Q_{\pi}(s, a)}{\partial \boldsymbol{\theta}} \\
&=\sum_{a} \frac{\partial \pi(a \mid s ; \boldsymbol{\theta}) \cdot Q_{\pi}(s, a)}{\partial \boldsymbol{\theta}} \\
&=\sum_{a} \frac{\partial \pi(a \mid s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \cdot Q_{\pi}(s, a)
\end{aligned}
$$
第一步到第二步是把求导拿到里面, 和的导数变成导数的和. 为了方便推导和理解, 第二步到第三步做了一个不正确的简化, 假设$Q_\pi(s, a)$ 和$\boldsymbol{\theta}$ 无关, 所以$Q_\pi$ 视为常数拿出来.

实际上这种假设对最终结果影响不大, 只是前面相差一个系数, 在梯度上升时会被学习率$\beta$ 吸收.

如果动作都是离散的, 推导到这里已经能够算出策略梯度了. 但实际应用时不会用这个公式来计算策略梯度, 而且这种形式没法处理连续的动作.

书接上文, 继续推导:
$$
\begin{aligned}
\frac{\partial V(s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} &=\sum_{a} \frac{\partial \pi(a \mid s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \cdot Q_{\pi}(s, a) \\
&=\sum_{a} \pi(a \mid s ; \boldsymbol{\theta}) \cdot \frac{\partial \log \pi(a \mid s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \cdot Q_{\pi}(s, a) \\
&= \mathbb{E}_A\left[ \frac{\partial{\log \pi(A \mid s ; \boldsymbol{\theta})}}{\partial \boldsymbol{\theta}} \cdot Q_{\pi}(s, A)\right]
\end{aligned}
$$
第一步到第二步正推不好推, 但逆着比较好验证, 首先是链式法则有:
$$
\frac{\partial \log \left[\pi(\boldsymbol{\theta})\right]}{\partial \boldsymbol{\theta}}=\frac{1}{\pi(\boldsymbol{\theta})} \cdot \frac{\partial \pi(\boldsymbol{\theta})}{\partial \boldsymbol{\theta}}
$$
然后两边同乘$\pi(\boldsymbol{\theta})$:
$$
\pi(\boldsymbol{\theta}) \cdot \frac{\partial \log \left[\pi(\boldsymbol{\theta})\right]}{\partial \boldsymbol{\theta}}=
\cancel{\pi(\boldsymbol{\theta})} \cdot \frac{1}{\cancel{\pi(\boldsymbol{\theta})}} \cdot \frac{\partial \pi(\boldsymbol{\theta})}{\partial \boldsymbol{\theta}} = \frac{\partial \pi(\boldsymbol{\theta})}{\partial \boldsymbol{\theta}}
$$
第二步到第三步比较好理解, 形式上就是把动作看成随机变量求期望.

Calculate Policy Gradient

Policy Gradient for Discrete Actions

先来看看第一种形式的策略梯度要如何计算. 如果Action是离散的, 设动作空间$\mathcal{A}=\{\text{“left”}, \text{“right”}, \text{“up”} \}$, 第一种形式:
$$
\frac{\partial V(s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} =
\sum_{a} \frac{\partial \pi(a \mid s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \cdot Q_{\pi}(s, a)
$$

对于每个动作$a \in \mathcal{A}$, 令$\mathbf{f}(a, \boldsymbol{\theta})=\frac{\partial \pi(a \mid s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \cdot Q_{\pi}(s, a)$.
策略梯度$\frac{\partial V(s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} = \mathbf{f}(\text{“left”}, \boldsymbol{\theta}) + \mathbf{f}(\text{“right”}, \boldsymbol{\theta}) + \mathbf{f}(\text{“up”}, \boldsymbol{\theta}) $.

Policy Gradient for Continuous Actions

上面那种形式对于连续的Action就比较麻烦了, 假设$\mathcal{A} = [0, 1]$, 第二种形式:
$$
\frac{\partial V(s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} = \mathbb{E}_{A \sim \pi(\cdot|s;\boldsymbol{\theta})}\left[ \frac{\partial{\log \pi(A \mid s ; \boldsymbol{\theta})}}{\partial \boldsymbol{\theta}} \cdot Q_{\pi}(s, A)\right]
$$
定积分没法求解这个期望, 因为$\pi$ 是个神经网络, 所以我们只能用蒙特卡洛近似:

根据$\pi(\cdot \mid s;\boldsymbol{\theta})$ 抽样得到一个随机动作$\hat{a}$,
令$\mathbf{g}(\hat{a}, \boldsymbol{\theta}) = \frac{\partial{\log \pi(A \mid s ; \boldsymbol{\theta})}}{\partial \boldsymbol{\theta}} \cdot Q_{\pi}(s, A)$, 直接算$\mathbf{g}(\hat{a}, \boldsymbol{\theta})$ 就行了.
根据$\mathbf{g}(\hat{a}, \boldsymbol{\theta})$ 的定义, 直接有$\mathbb{E}_{A}[\mathbf{g}(A, \boldsymbol{\theta})]=\frac{\boldsymbol{\partial} V(s ; \boldsymbol{\theta})}{\boldsymbol{\partial} \boldsymbol{\theta}}$, 因为$\hat{a}$ 是从$\pi(\cdot\mid s;\boldsymbol{\theta})$ 里抽出来的, 所以$\mathbf{g}(\hat{a}, \boldsymbol{\theta})$ 就是策略梯度$\frac{\boldsymbol{\partial} V(s ; \boldsymbol{\theta})}{\boldsymbol{\partial} \boldsymbol{\theta}}$ 的无偏估计. 故$\mathbf{g}(\hat{a}, \boldsymbol{\theta})$ 就是$\frac{\boldsymbol{\partial} V(s ; \boldsymbol{\theta})}{\boldsymbol{\partial} \boldsymbol{\theta}}$ 的近似.

这种方法对离散动作也适用.

Update Policy Network using Policy Gradient

我们已经推导出了策略梯度, 和如何用策略梯度更新策略网络, 现在来梳理一下:

观察状态$s_t$.
用蒙特卡洛从$\pi(\cdot \mid s;\boldsymbol{\theta})$ 中抽样出随机动作$a_t$.
计算价值函数的值$q_t\approx Q_\pi(s_t, a_t)$.
对策略网络$\pi$ 求导, 计算$\mathbf{d}_{\boldsymbol{\theta}, t}=\left.\frac{\partial \log \pi\left(a_{t} \mid s_{t}, \boldsymbol{\theta}\right)}{\partial \boldsymbol{\theta}}\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}_{t}}$.
近似计算策略梯度$\mathbf{g}\left(a_{t}, \boldsymbol{\theta}_{t}\right)=q_{t} \cdot \mathbf{d}_{\theta, t}$.
用策略梯度更新策略网络: $\boldsymbol{\theta}_{t+1}=\boldsymbol{\theta}_{t}+\beta \cdot \mathbf{g}\left(a_{t}, \boldsymbol{\theta}_{t}\right)$.

等会… 是不是还有个问题, $q_t$ 怎么求来的? 我们只能用以下两种方法来近似$q_t$:

Reinforce(蒙特卡洛策略梯度):
- 在一个Episode中, 记录下迹, 就能获得所有时刻$t$ 时的回报$u_t=\sum^T_{k=t} \gamma^{k-t} r_k$,
- 由于$Q_\pi(s_t, a_t) = \mathbb{E}[U_t]$, 所以我们用观测值$u_t$ 来近似$Q_\pi(s_t, a_t)$, 即$q_t = u_t$.
Actor - Critic:
- 贯彻神经网络近似一切的传统, 用一个新的神经网络来近似$Q_\pi$, 这样就有俩神经网络, 一个是Actor, 另一个是Critic, 这也就是Actor - Critic Method.

Actor - Critic Method

前面说过, 由于策略梯度$\frac{\partial V(s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}}$求解需要用到动作价值函数$Q_\pi$, 在策略学习中用Reinforce方法可以求得.

如果使用神经网络来近似动作价值函数$Q_\pi$, 这就催生了Actor - Critic Method, 把价值学习和策略学习结合到一起:

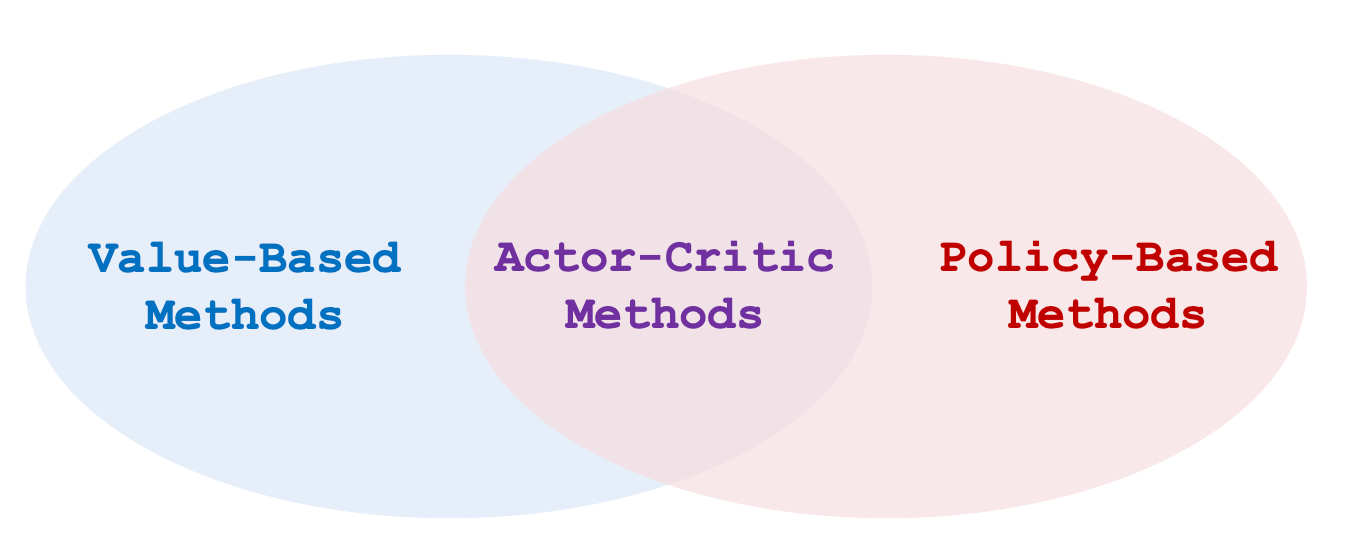
State - Value Function Approximation

在价值学习时, 我们把策略函数$ \pi\left(a \mid s\right) $ 用策略网络$ \pi\left(a \mid s;\boldsymbol{\theta}\right) $ 来近似, 我们只需要类似的把动作价值函数$Q_\pi{s, a}$ 用Value Network(价值网络)$q(s, a; \mathbf{w})$ 来表达即可:
$$
V_{\pi}\left(s\right) =\sum_{a \in \mathcal{A}} \pi\left(a \mid s\right) \cdot Q_{\pi}\left(s, a\right) \approx \sum_{a \in \mathcal{A}} \pi\left(a \mid s;\boldsymbol{\theta}\right) \cdot q(s, a;\mathbf{w})
$$
$\boldsymbol{\theta}, \mathbf{w}$ 分别为Policy Network, Value Network的参数.

Policy Network (Actor)

Policy Network近似了策略函数$\pi(a\mid s)$, 继续沿用我们之前讲过的结构吧:

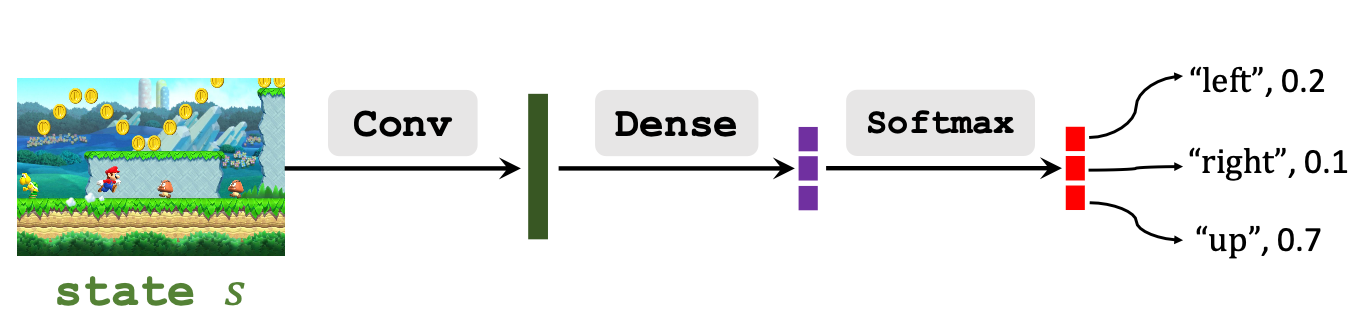
Policy Network的输出是在状态$s$ 下选择各个动作$a$ 的概率, $\sum_{a\in \mathcal{A}}\pi(a \mid s; \boldsymbol{\theta})=1$.

Value Network (Critic)

Value Network近似了动作价值函数$Q_\pi(s, a)$, 根据$s$ 对所有的$a$ 打分.

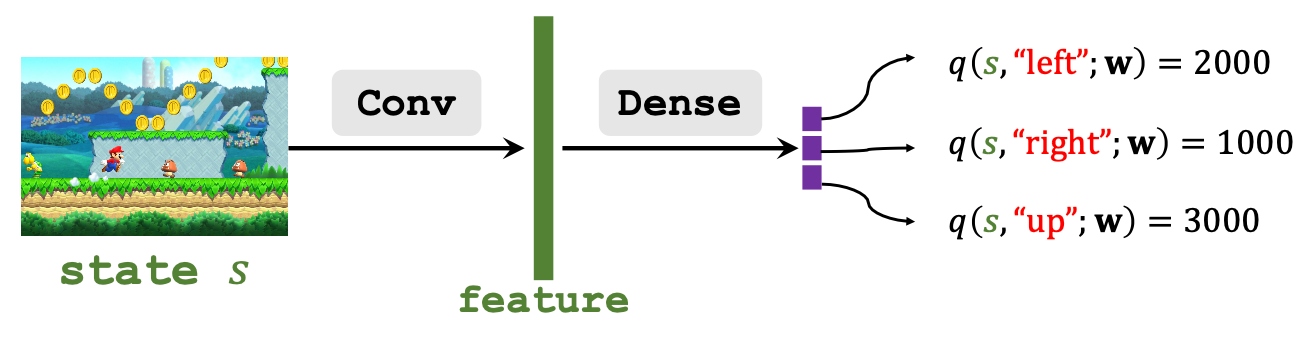
虽然Value Network和DQN有相同的网络结构, 但Value Network近似的是动作价值函数$Q_\pi(s, a)$, 而不是最优动作价值函数$Q^\star(s, a)$, 因为在Actor - Critic Method中, Agent的动作由Policy Network决定, 而不是由Value Network自身决定.

Value Network的输出是在状态$s$ 下各动作$a$ 的打分.

Actor Critic

Policy Network像演员一样, 根据策略做出相应的动作, 而Value Network像评委一样, 评价演员的动作好坏:

随着网络的训练, 演员的动作越来越好, 裁判的打分越来越精准.

如果只是从网络结构的角度来看, GAN与它几乎是相同的! Actor对应着GAN的Generator, Critic对应着GAN的Discriminator. 和GAN类似的, 在训练后, Value Network会被丢弃.
但是突然想起GAN是一个十分难训练的网络… 估计这个问题也会在Actor - Critic上也存在. 如果从时间线上来看, Actor - Critic比GAN要早! 所以到底是谁比较像谁呢?

Train the Neural Network

请回顾TD算法和策略梯度.

怎么才能训练这两个网络呢? 我们来观察一下Actor - Critic 的状态价值函数:
$$
V(s; \boldsymbol{\theta}, \mathbf{w}) = \sum_{a \in \mathcal{A}} \pi\left(a \mid s;\boldsymbol{\theta}\right) \cdot q(s, a;\mathbf{w})
$$

更新Policy Network $\pi\left(a \mid s;\boldsymbol{\theta}\right)$ 是为了让状态价值$V(s; \boldsymbol{\theta}, \mathbf{w})$ 更大, 令演员得到的平均分更高. 所以Policy Network学习时, 依赖的价值是有监督的由Value Network提供的.
更新Value Network $q(s, a;\mathbf{w})$ 是为了对演员动作的打分更为精准, 从而更好估计Return. 所以Value Network学习时, 依赖的奖励是有监督的由环境提供的.

Actor观察状态$s$ 后, 做出动作$a$, Critic根据$s$ 和$a$, 给出打分$q$. 然后环境状态转移, 同时给予奖励$r$. Critic从环境奖励中吸取经验改进自己, 演员也根据评委的意见改进自己, 然后如此循环:

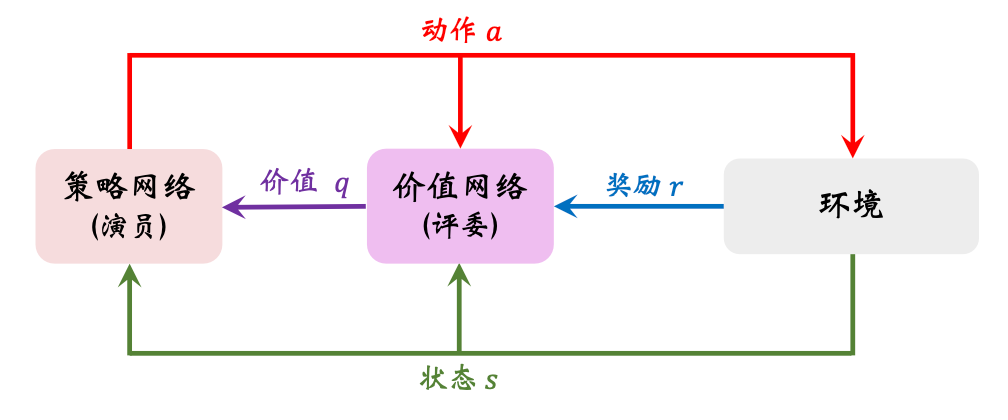
为了让评委越来越好, 评委根据$s, a, r$ 来改进自己的打分$q$. 可以让评委比较相邻两次的打分$q_t, q_{t+1}, r_t$, 使用TD算法更新参数.
为了让演员越来越好, 演员根据$q$ 来改进自己在不同$s$ 下选择$a$ 的能力. 如果裁判很辣鸡, $q$ 就会不准确, 演员为了迎合评委的口味, 自身也会跑偏.

架子搭好了, 我们把具体的计算流程往里面填充:

观察状态$s_t$, 并从$\pi\left(\cdot \mid s_t;\boldsymbol{\theta}_t\right)$ 中随机抽样得到动作$a_t$.
令Agent做出动作$a_t$, 同时得到新的环境状态$s_{t+1}$ 和奖励$r_t$.
从$\pi\left(\cdot \mid s_{t+1};\boldsymbol{\theta}_t\right)$ 随机采样出假设要做出的动作$\tilde{a}_{t+1}$, 但并不执行$\tilde{a}_{t+1}$.
为了使用TD算法, 计算两次Value Network的输出$q_t = q(s_t, a_t;\mathbf{w}_t), q_{t+1}=q(s_{t+1}, \tilde{a}_{t+1}; \mathbf{w}_t)$.
计算TD Error, $\delta_t=q_t - (r_t + \gamma\cdot q_{t+1})$, $r_t + \gamma\cdot q_{t+1}$ 即为TD Target.
计算Value Network的导数$\mathbf{d}_{w, t}=\left.\frac{\partial q\left(s_{t}, a_{t} ; \mathbf{w}\right)}{\partial \mathbf{w}}\right|_{\mathbf{w}=\mathbf{w}_{t}}$
用TD算法梯度下降更新Value Network, $\mathbf{w}_{t+1} = \mathbf{w}_t - \alpha \cdot \delta \cdot \mathbf{d}_{w, t}$.
计算Policy Network的导数$\mathbf{d}_{\theta, t}=\left.\frac{\partial \log \pi\left(a_{t} \mid s_{t}, \boldsymbol{\theta}\right)}{\partial \boldsymbol{\theta}}\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}_{t}}$.
用策略梯度上升来更新Policy Network, $\boldsymbol{\theta}_{t+1}=\boldsymbol{\theta}_t + \beta \cdot q_t \cdot \mathbf{d}_{\theta, t}$.

第九步中很多书和论文都写成$\boldsymbol{\theta}_{t+1}=\boldsymbol{\theta}_t + \beta \cdot \delta_t \cdot \mathbf{d}_{\theta, t}$, 这么写称为Policy Gradient with Baseline, 一般使用Baseline效果更好. 二者期望完全相等, 虽不影响期望, 但是好的Baseline可以降低方差, 加快收敛.
事实上, 只要接近$q_t$ 的数都能设定为Baseline, 只要它不是动作$a_t$ 的函数.

AlphaGo!

注: 本节中讲解的细节和AlphaGo原论文并不一致, 做了相应的简化.

AlphaGO在2016年击败了世界围棋冠军李世石, 这在当时是一件非常轰动的事情, 各大媒体更是把AI吹上天了.

Go Game

围棋棋盘上共有$19 \times 19=361$ 个点, 我们先把RL中的相关概念抽象出来:

State: 按照黑白二子在棋盘上的位置来区分, 它的状态可以是$19 \times 19 \times 2$ 的张量, 其值全部为0或1, 用来表示黑 / 白子是否在该位置有子. 实际上AlphaGo使用了更大的状态张量$19 \times 19 \times 48$来存储其他信息.
Action: 状态空间$\mathcal{A}$ 自然就为棋盘上的361个位置, 即$\mathcal{A} = \set{1, 2, 3 \dots, 361}$.

整场游戏可能选择的策略是一个Action Sequence, 非常非常大.

High Level Ideas

从比较高的视角来看, AlphaGo通过三步来训练自己:

用Behavior Cloning来初始化训练Policy Network. 其实它是监督学习, 从人类的对战中学习到.
用Reinforcement Learning的策略梯度进一步训练Policy Network, 让两个Policy Network互相对战.
训练完Policy Network后再训练Value Network.

在对战李世石时使用的实际上不是Policy Network来做动作, 而是借助Policy Network和Value Network的指导做Monte Carlo Tree Search(MCTS, 蒙特卡洛树搜索) 来做出最终决策的.

Policy Network

State

AlphaGo有多个版本, 采用的State不一样.

最初版本的AlphaGo(后文称之为AlphaGo初号机)用$19 \times 19 \times 48$ 的张量表示棋盘状态.

最新版本的AlphaGo Zero用$19 \times 19 \times 17$ 的张量作为状态, 这个更好解释:

$19 \times 19$ 描述的棋盘的所有位置, 共有17个$19 \times 19$的矩阵.
把当前黑子的位置, 和之前7步黑子的位置, 用8个$19 \times\ 19$ 的矩阵来表示.
把当前白子的位置, 和之前7步白子的位置, 用8个$19 \times\ 19$ 的矩阵来表示.
最后一个矩阵, 也就是图中最下面那个矩阵, 是黑白子指示矩阵, 如果该黑子走了则矩阵全是1, 白子走全是0.

具体为什么是把之前7步的位置信息整合在一起, 应该是理解为实验超参.

Policy Network Architecture

AlphaGo Zero的策略网络结构是这样的:

就是CNN先提取特征, 然后直接加一个全连接获取动作概率.

AlphaGo初号机的策略网络结构就比较简单了:

直接就只使用了CNN.

Behavior Cloning

AlphaGo初号机使用了Behavior Cloning.

因为Policy Network开始随机初始化, 网络参数不太好, 探索环境需要花很久很久的时间, 所以给策略网络一个比较好的初始引导是比较重要的, 这样能给网络一个比较好的初始解. 如果把人类游戏录像给AlphaGo看, 它就能够在初期模仿人类的游戏行为.

刚巧, 有一个人类围棋的数据集KGS, 拥有16w条围棋游戏记录, 作为训练数据, 让AlphaGo学习.

Behavior Cloning不是强化学习, 而是一种模仿学习(Imitation Learning), 这种方法与奖励无关. 下面来在场景下来介绍一下它的执行流程:

观察State $s_t$.
用策略网络针对$s_t$ 做个决策: $\mathbf{p}_{t}=\left[\pi\left(1 \mid s_{t}, \boldsymbol{\theta}\right), \cdots, \pi\left(361 \mid s_{t}, \boldsymbol{\theta}\right)\right] \in(0,1)^{361}$.
假设下一步人类玩家做出的动作$a_t^\star=281$, 同时将其编码为One hot标签$y_t \in \set{0, 1}^{361}$.
对$y_t, \mathbf{p}_t$ 用CrossEntropy作为Loss, 梯度下降更新策略网络参数.

其实就是把每个时间步的人类围棋行为当做多分类问题, 用梯度下降训练了Policy Network, 对吧?

Behavior Cloning后AlphaGo已经能碾压围棋小白了, 为啥呢? 大概率是因为$s_t$ 在AlphaGo看过的棋局里面出现过.

那为啥还在后面要用RL来强化AlphaGo呢? 因为$s_t$ 可能没有出现在AlphaGo看过的棋局里面. 如果没出现过, 策略网络可能直接就傻了, 做出的$a_t$ 不会太好, 所谓一步错步步皆错, 正是因为某个$a_t$ 导致策略网络进入了没见过的棋局, 后面做出的错误都会慢慢累加, 导致下棋下的越来越差, 最终输掉棋局, 尤其是在围棋庞大的棋局局势规模下, 该缺点尤为明显.

事实上, AlphaGo Zero没有使用Behavior Cloning, 能打爆AlphaGo初号机. 以现在的目光来看可能在围棋游戏中模仿人类的思路去下棋对Agent是有害的, 可能不利于养成它自己的思路. 当然也仅限于围棋中, 有些零容错场景Behavior Cloning依然强大, 比如无人驾驶, 手术机器人等.

Train Policy Network Using Policy Gradient

如果用RL来训练策略网络, 必须要有Agent和Environment:

这里的Player作为Agent, 它的参数是每一局过后都会更新的. 而Opponent作为Environment, 它的参数不需要更新, 只需要从过去的Policy Network参数里面随便选一个就好.

Reward

用RL训练Agent还需要奖励. 加入$T$ 时刻游戏结束, 定义如下奖励$r$:

$r_1 = r_2 = r_3 = \cdots = r_{T-1}=0$.
$r_T = + 1$ (Winner).
$r_T = -1$ (Loser).

这里定义的Return 不使用折扣, 即$u_t = \sum_{i=t}^T r_i$. 那么Winner的Return就为$u_1 = u_2 = u_3 = \cdots = u_{T}=+1$, Loser的Return为$u_1 = u_2 = u_3 = \cdots = u_{T}=-1$.

策略梯度的推导在前面已经讲过了. 我们可以用前面讲过的Reinforce方法来用$u_t$ 近似$Q_\pi(s_t, a_t)$, 策略梯度为就可以近似为$\frac{\partial \log \pi(a_t \mid s_t, \boldsymbol{\theta})}{ \partial \boldsymbol{\theta}} \cdot u_t$, 直观来看就是说如果赢了每步棋下的都是对的, 输了每步都是错的.

我们来概括一下策略网络的训练:

让两个策略网络相互博弈, Agent所使用的策略网络每一把都更新一次参数.
一局打完后会获得一个迹$s_1, a_1, s_2, a_2, \cdots, s_T, a_T$, 以及输赢所对应的$u_T$.
知道这一把的结果和回报后, 求出每一把策略梯度总和$\mathbf{g}_{\theta}=\sum_{t=1}^{T} \frac{\partial \log \pi\left(a_{t} \mid s_{t}, \boldsymbol{\theta}\right)}{\partial \boldsymbol{\theta}} \cdot u_{t}$.
策略梯度上升 $\boldsymbol{\theta} \leftarrow \boldsymbol{\theta} + \beta \cdot \mathbf{g}_\theta$.

这时候策略网络已经比较强了, 但还不够强, 会犯一些小错误, 所以才不使用策略网络做决策, 而是以它为依据, 辅助MCTS做决策.

Value Network

前面讲的价值网络是为了近似动作价值函数$Q_\pi(s, a)$, 而在AlphaGo中直接使用价值网络$v(s ; \mathbf{w})$ 近似价值函数$V_\pi(s)$. 在我们定义的回报$U_t$ 中, $V_\pi(s) = \mathbb{E}\left[U_t \mid S_t = s\right]$ 会给出$\left[-1, 1\right]$ 之间的值, 当$V_\pi$ 快逼近-1时说明快输了, +1说明快赢了. MCTS需要借助价值网络来做决策.

在AlphaGo 初号机中, 策略网络和价值网络是两个分开的网络. 但在Alpha Zero中已经共享了策略网络和价值网络对状态的抽取过程, 即卷积部分是共享的.

策略网络和价值网络是分开训练的, 因此它不能算做是Actor - Critic.

价值网络训练流程如下:

仍然是让两个策略网络互相打, 还是赢了的回报为+1, 输了的为-1. 不更新策略网络的参数.
我们希望观测到的回报和价值网络预测的价值相同, 所以使用MSE作为损失函数优化, 即$L=\sum_{t=1}^{T} \frac{1}{2}\left[v\left(s_{t} ; \mathbf{w}\right)-u_{t}\right]^{2}$.
用梯度下降优化价值网络参数, $\mathbf{w} \leftarrow \mathbf{w} - \alpha \cdot \frac{\partial L}{\partial \mathbf{w}}$.

至此, AlphaGo的训练就结束了.

Monte Carlo Tree Search

用Behavior Cloning和Policy Gradient训练完Policy Network, 用Gradient Descent训练完Value Network后, 在真正Inference的时候用的不是前面的二者, 而是使用的蒙特卡洛树搜索(Monte Carlo Tree Search).

用人类的习惯去思考一下, 这样做确实是有一些道理的. 因为我们在下棋的时候, 经常思考, 我们这一步走了$a_t$, 对手会怎么走出下一步呢 ($s_{t+1}$)? 假如对手按$s_{t+1}$ 走了, 这种局势对我好不好, 那我下一步该怎么走呢($a_{t+1}$)? 这样思考可以确保局势在自己的掌控之中, 不落入对手的圈套. 计算机强大的计算能力导致它十分擅长做这种搜索, 曾经97年的深蓝就是这么做的, 当时深蓝能一次性的暴力穷举出之后的12步.

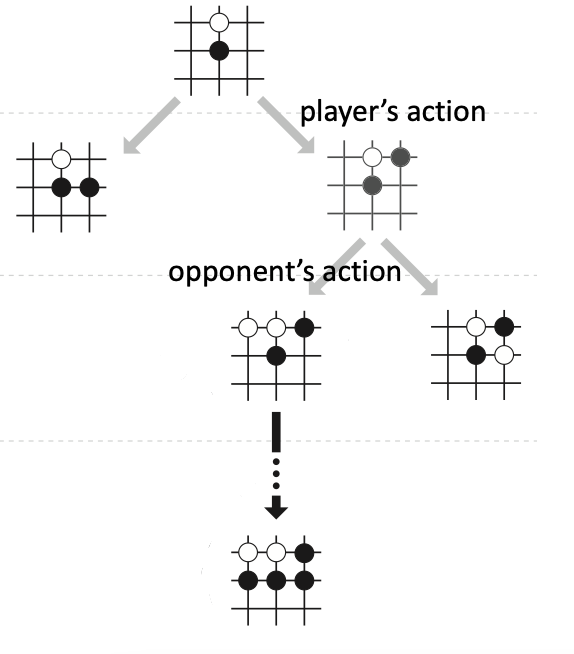
搜索的大概想法是:

根据策略网络给出的动作好坏筛选一些好的动作, 随机选择一个动作$a$.
让策略网络根据选择的$a$ 做自我博弈, 直到游戏结束, 看看输赢.
如此反复, 直到所有好的动作都被穷举完.
每个动作$a$ 都应该对应着一个打分, 每回选择最高分数的作为真正要执行的动作.

MCTS以上述四个过程为原型执行.

Step 1: Selection

观测到$s_t$, 有很多位置都可以放棋子, 但是并不是每个位置都值得考虑, 否则那样搜索空间太大了, 可以根据动作的好坏程度来选择.

首先, 给所有有效动作$a$ 打分, 计算方式如下:
$$
\operatorname{score}(a) = Q(a) + \eta \cdot \frac{\pi(a \mid s_t; \boldsymbol{\theta})}{1 + N(a)}
$$
其中有:

$Q(a)$: 它是一张搜索记录计算出来的动作价值表, 后面会解释.
$\pi(a \mid s_t; \boldsymbol{\theta})$: 策略网络根据$s_t$ 选择的动作$a$的概率.
$N(a)$: 对于$s_t$, $a$ 已经被探索过的次数, 这样可以减少$a$ 被过多探测的次数.
$\eta$: 超参数, 作为加权系数.

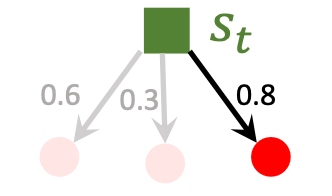
然后, 假如计算出三个动作的打分分为0.6, 0.3, 0.8, 则只会选择分数最大的动作作为假定要执行的动作$a_t$.

Step 2: Expansion

根据假定做出的动作$a_t$, AlphaGo会揣测对手做出的动作$a^\prime_t$, 这对于AlphaGo来说会导致出现新的环境状态$s_{t+1}$. 这样的推测肯定也必须是有依据的, 采用换位思考的思路, AlphaGo会用自己的策略网络来抽样得出一个对手动作$a_t^\prime$:
$$
a_t^\prime \sim \pi(\cdot \mid s_t^\prime; \boldsymbol{\theta})
$$
$s_t^\prime$ 指的是对手视角的状态.

这里对手相当于Agent的环境, 其状态转移函数$p(s_{t+1} \mid s_t , a_t)$ 当然是未知的, 但是我们可以换位思考, 使用$\pi$ 来代替它.

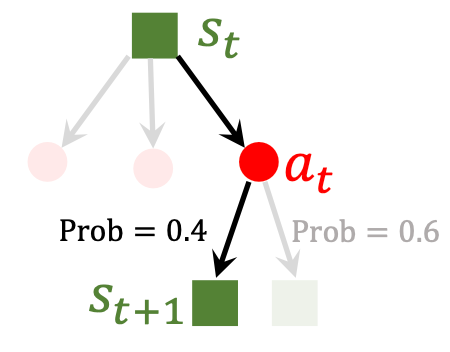
这样在抽样得出的对手动作$a_t^\prime$ 影响下, 我方观察到的状态为$s_{t+1}$.

Step 3: Evaluation

从$s_{t+1}$ 开始, 后面都是策略网络的自我博弈, 也就是Fast Rollout:

Player: $a_k \sim \pi(\cdot \mid s_k; \boldsymbol{\theta})$.
Opponent: $a_k^\prime \sim \pi(\cdot \mid s_k^\prime; \boldsymbol{\theta})$.
当分出胜负时, 赢了则$r_T=+1$, 输了$r_T=-1$. 这种奖励可以一定程度评价$s_{t+1}$ 的好坏. 应该想办法令赢了增加状态$s_{t+1}$ 的评分, 反之降低.

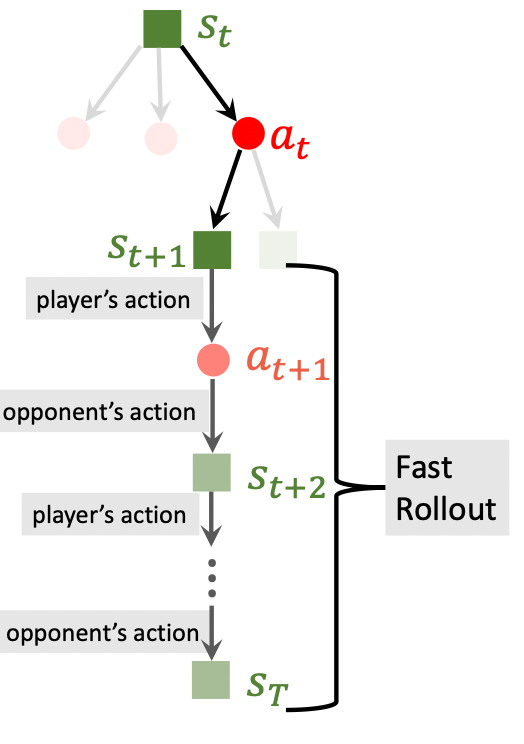
除了用$r_T$ 来判断状态好坏, AlphaGo还用价值网络$v$ 来评价$s_{t+1}$:

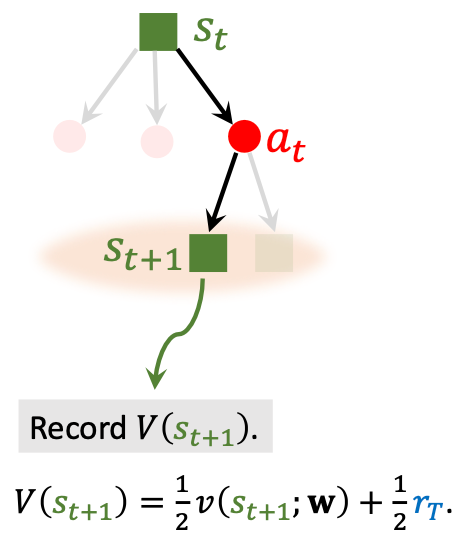
把价值网络给出的$s_{t+1}$ 评分$v(s_{t+1}; \mathbf{w})$ 和$r_T$ 做个平均再加在一起, 作为$s_{t+1}$ 的分数, 并记录下来.

$s_{t+1}$ 越好, $V(s_{t+1})$ 就越高, 如果往回追溯, $a_t$ 动作就越好.

Step 4: Backup

由于各类随机性, Evaluation会反复模拟很多次, 所以每个动作$a_t$ 下都会有很多组不同状态$s_{t+1}$ 对应的$V(s_{t+1})$:

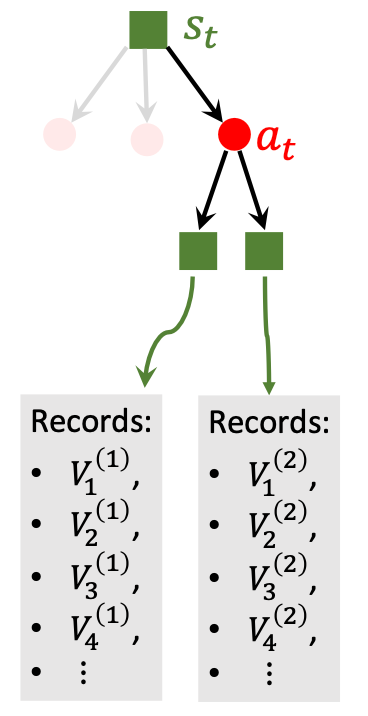
在我们Step 1中提到的动作价值$Q(a_t)$ 就可以被状态价值$V(s_{t+1})$ 所表示了:
$$
Q(a_t)= \operatorname{mean}(\text{recorded } V\text{‘s})
$$
初始时, 还没有被记录下来的$V$, 那么$Q$ 初始化时都为0.

回想一下我们在Step 1中写过的打分式:
$$
\operatorname{score}(a) = Q(a) + \eta \cdot \frac{\pi(a \mid s_t; \boldsymbol{\theta})}{1 + N(a)}
$$
这意味着两点:

刚开始时$Q(a)$ 都为0, 所以基本上依赖后一项, 也就是策略网络给出的打分来判断动作$a$ 好坏.
随着模拟次数增加, 策略网络觉得越好的动作就越有可能被选中, 即$N(a)$ 变大, 第二项缩小, 后期会主要依赖动作价值$Q(a)$ 来评价动作好坏.

Decision Making after MCTS

前面说过, 一个动作越好, 它的$Q(a), \pi(a)$, 都会越大, 它的$\operatorname{score}$ 也就高, 被选中的几率就越大, 即$N(a)$ 越大.

AlphaGo做决策很简单, 就是选择被选中次数最多的动作作为实际所选择的动作$a_t$:
$$
a_{t}=\underset{a}{\operatorname{argmax}} N(a)
$$

既然每次选择的都是$N(a)$ 最大的动作, 它也与动作$a$ 本身的好坏有关, 要是策略网络能强大到和费那么老大劲的搜索一样就好了. 直觉告诉我们, MCTS做了非常多次采样模拟才得到的决策应该比策略网络一股脑给出的决策要好一些, 因此具有指导意义.
没错, AlphaGo Zero的想法是把所有$a$ 对应的$N(a)$ 都归一化, 视为概率分布, 最小化其与策略网络给出的动作概率分布的交叉熵, 这样MCTS在训练过程中也可以参与到策略网络的优化过程中.

至此, AlphaGo的讲解结束. 这不禁让我想起这样一幅图: