支持向量机SVM Support Vector Machine
SVM是一个监督学习下运作的线性分类器. 但是由于核技巧的存在, 使得它本质上成为一个非线性分类器. 因为SVM涉及到很多关于凸优化的内容, 我自己本身不是很了解, 所以尽可能的避开这些内容, 以大致了解工作原理为基准.
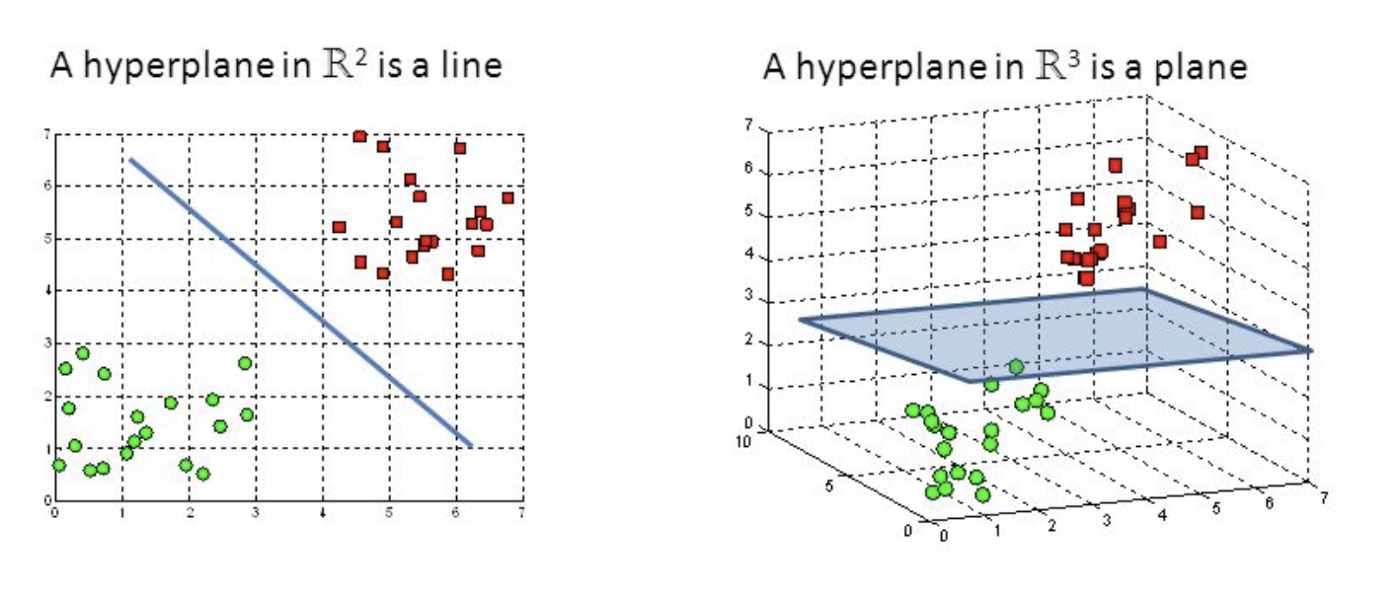
SVM的目标就是寻找一个最优超平面, 使得数据能够被这个超平面分开. 超平面这个概念可以由三维和二维进行递推, 在二维空间中的超平面就是一维的, 即一条线, 在三维空间中的超平面是一个二维的平面. 那么以此类推, 在N维空间中的超平面是N-1 维平面.
把超平面定义为:
$$
f(x)=\operatorname{sign}(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b)
$$sign的意思是说, 在超平面上面取正号, 下方取负号. 那么很明显$w$ 是法向量, $b$ 是位移项.
SVM的优化理念是最大化超平面到各类样本之间的距离, 使得这个超平面能够成功分开各类, 并且离这些样本点尽可能的远. 为什么要最大化这个间距呢? 因为在真实数据中的误差可能会干扰实际的预测效果, 间距大意味着更强的鲁棒性. 即使加入了一些噪声, 也会因为含有间距而不导致或尽可能少的导致预测错误.
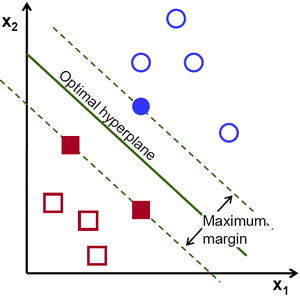
把支撑超平面的点(距离超平面最近的样本点)叫做支持向量, 也就是图中的超平面旁的实心红色方块和实心蓝色圆. 一般情况下, 最佳超平面一定是到两边支持向量距离相等的那个.
硬间隔 Hard Margin
硬间隔SVM被转化为一个寻找最大间隔超平面的数学问题, 所以Hard Margin SVM也被称为最大间隔分类器.
样本空间中的样本$x$到超平面的距离$r$ 可以表示为:
$$
r=\frac{\left|\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b\right|}{|\boldsymbol{w}|}
$$
如果超平面能正确分类样本, 则标签$y_i = +1$,对应的范围设为超平面上方, 标签$y_i = -1$,对应的范围设为超平面下方, 即:
$$
\left\{\begin{array}{ll}
\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b > 0, & y_{i}=+1 \\
\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b <0, & y_{i}=-1
\end{array}\right.
$$
若令间隔为1, 则上述约束更改为:
$$
\left\{\begin{array}{ll}
\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b \geqslant+1, & y_{i}=+1 \\
\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b \leqslant-1, & y_{i}=-1
\end{array}\right.
$$
那么相应的两个不同类的支持向量到超平面的距离为:
$$
\gamma=\frac{2}{|\boldsymbol{w}|}
$$
如下图所示:
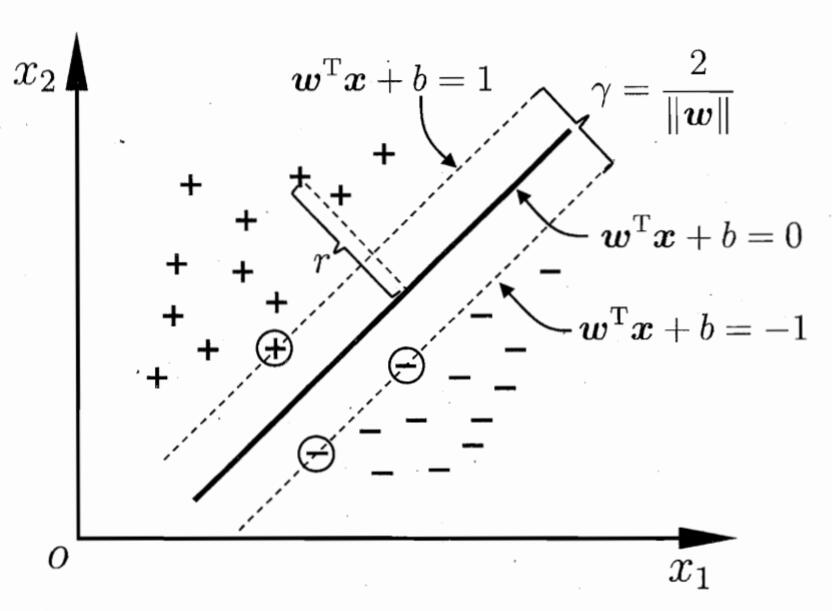
若想找到最大间隔划分超平面, 其实就是为了找到相应的$w$ 和$b$, 使得间距$\gamma$ 最大.
$$
\begin{aligned}
\max _{\boldsymbol{w}, b} & \frac{2}{|\boldsymbol{w}|} \\
\text { s.t. } & y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right) \geqslant 1, \quad i=1,2, \ldots, m
\end{aligned}
$$
最小化$|\boldsymbol{w}|^{-1}$的目标等同于最大化$|\boldsymbol{w}|^2$, 重写为:
$$
\begin{aligned}
\min _{\boldsymbol{w}, b} & \frac{1}{2}|\boldsymbol{w}|^2 \\
\text { s.t. } & y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right) \geqslant 1, \quad i=1,2, \ldots, m
\end{aligned}
$$
这就是SVM的基本形式.
其实满足约束的是一个凸二次规划问题, 计算量很大. 利用拉格朗日乘子法解决其对偶问题, 向上述约束添加拉格朗日乘子:
$$
L(\boldsymbol{w}, b, \boldsymbol{\alpha})=\frac{1}{2}|\boldsymbol{w}|^{2}+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)\right)
$$
那么对$\boldsymbol{w}$和$b$求偏导, 则得到:
$$
\boldsymbol{w} =\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{x}_{i} \quad
0 =\sum_{i=1}^{m} \alpha_{i} y_{i}
$$
带回原式将$\boldsymbol{w}$和$b$消去.
$$
\begin{aligned}
&\max _{\boldsymbol{\alpha}} \sum_{i=1}^{m} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} \boldsymbol{x}_{i}^{\mathrm{T}} \boldsymbol{x}_{j} \\
&\text { s.t. } \sum_{i=1}^{m} \alpha_{i} y_{i}=0 \\
& \alpha_{i} \geqslant 0, \quad i=1,2, \ldots, m
\end{aligned}
$$
如果能够解出来$\boldsymbol{\alpha}$ , 就能解出超平面:
$$
\begin{aligned}
f(\boldsymbol{x}) &=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b \\
&=\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{x}_{i}^{\mathrm{T}} \boldsymbol{x}+b
\end{aligned}
$$
解决非线性规划问题需要用到更一般的拉格朗日乘子法, 额外加上KKT(Karush-Kuhn-Tucker)条件:
$$
\left\{\begin{array}{l}
\alpha_{i} \geqslant 0 \\
y_{i} f\left(\boldsymbol{x}_{i}\right)-1 \geqslant 0 \\
\alpha_{i}\left(y_{i} f\left(\boldsymbol{x}_{i}\right)-1\right)=0
\end{array}\right.
$$
如果$\alpha_{i}>0$, 必有$y_if(\boldsymbol{x_i})=1$, 即该样本点位于最大间隔边界上.
利用SMO(Sequential minimal optimization, 序列最小优化算法), 求解其中的各个$\alpha_i$. SMO固定了$\alpha_i$以外的其他参数, 每次选取一对需要更新的$\alpha_i$和$\alpha_j$, 利用约束$\sum_{i=1}^{m} \alpha_{i} y_{i}=0$来得到更新后的$\alpha_i$和$\alpha_j$.
上述部分的数学推导有很多细节为了理解而省略了, 数学底子有些薄弱, 暂时无法细究. 日后会补上. 这部分也是面试时的核心, 尤其是对偶, 拉格朗日乘子法和KKT, SMO.
核函数 Kernel Function
这么搞一定会有些问题. SVM本来就是一个线性分类器, 假如样本分布真的是线性不可分的呢? 核函数和核技巧使得SVM具有一定的非线性分割能力. 通过核函数, 使得样本从低维映射到高维, 如果样本在高维空间中线性可分, 那么SVM就可以成功将样本分开.
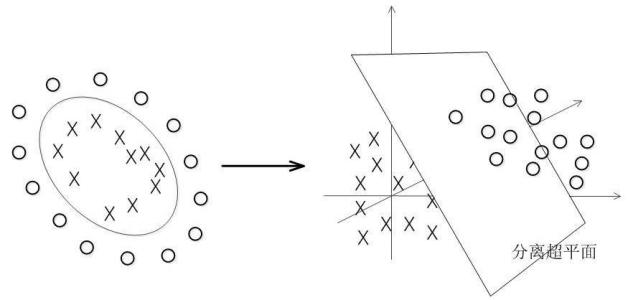
而核函数的定义实际上也隐式的定义了额外的特征空间, 使得这些特征在空间中线性可分. 所以和函数的选择和结果有着直接的关联, 它也是SVM里最大的变数. 文本数据一般采用线性核, 情况不明时可以先尝试高斯核.
软间隔 Soft Margin
在现实任务中收集的数据很难确定核函数, 即便找到了某个核函数使得所有训练数据在特征空间中线性可分, 也很难确定这个结果是不是过拟合造成的. 缓解该问题的办法是允许SVM在样本划分时出现一些错误, 引入软间隔的概念.

与硬间隔相比, 软间隔的优化目标更加的松弛, 体现在对约束条件加入松弛变量.
$$
\begin{aligned}
&y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)\geq 1-\xi_{i}, \quad \xi_{i} \geq 0 \\
&\min \sum_{i=1}^m \xi_i
\end{aligned}
$$
那么相应的优化目标也变为:
$$
\begin{array}{cl}
\min\limits_{w, b, \xi_i} & \frac{1}{2}|\boldsymbol{w}|^{2}+C \sum\limits_{i=1}^{n} \xi_{i} \\
\text {s.t.} & y_{i}\left(\boldsymbol{w}^{T} \boldsymbol{x}_{i}+b\right) \geq 1-\xi_{i} \\
& \xi_{i} \geqslant 0 \quad i=1,2, \cdots, n
\end{array}
$$
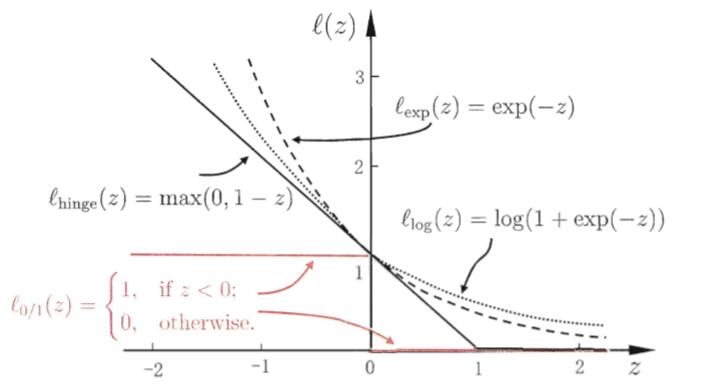
松弛变量$\xi_i$ 为可替换的损失函数, 一般使用hinge损失, 对数损失, 指数损失.