本文介绍了Pointer Network, CopyNet, Pointer-Generator Network以及Coverage机制在文本摘要与对话系统中的应用, 既可以作为知识点介绍, 也可以作为论文阅读笔记. 此外, 该部分内容为外部知识引入NLP任务中提供了思路.
本文阅读所需的前置知识包括:
- Seq2Seq
- Attention
- Bi - directional RNN
Pointer Network
指针网络出自Pointer Networks. 在Seq2seq中, 经常有一种模型输出严重依赖输入的问题, 一旦问题规模发生变化, 那就必须重新训练网络. 作者利用Attention机制和Seq2Seq进行结合, 克服了这个问题.
“输出严重依赖输入”指的是输出往往是输入的子集. 比如在机器翻译中, 输出向量大小必须取决于字典长度, 并不能根据Encoder输入内容而发生变化. 在求凸包(Convex Hull)问题中, 输入和输出都是坐标序列, 规模是不固定的. 可变大小序列的排序和各种组合优化都是这类问题.
凸包是计算图形学中的概念, 通俗一点说凸包问题就是根据给定的二维平面点集找到能够包含点集中所有点的最外层点的连接线.
而”指针”的命名来自于其Attention产生的权重直接决定了Decoder的输出对应着哪个Encoder的数据输入, 这样输出就从输入中进行选择, 能很好的解决该问题. 该结构非常简单, 与加权平均的注意力机制不同, Ptr - Net并非将Attention机制对信息进行筛选, 而是直接指出输出信息. 指针网络直接将Attention的权重最高者直接作为Decoder的输出, 如下图:
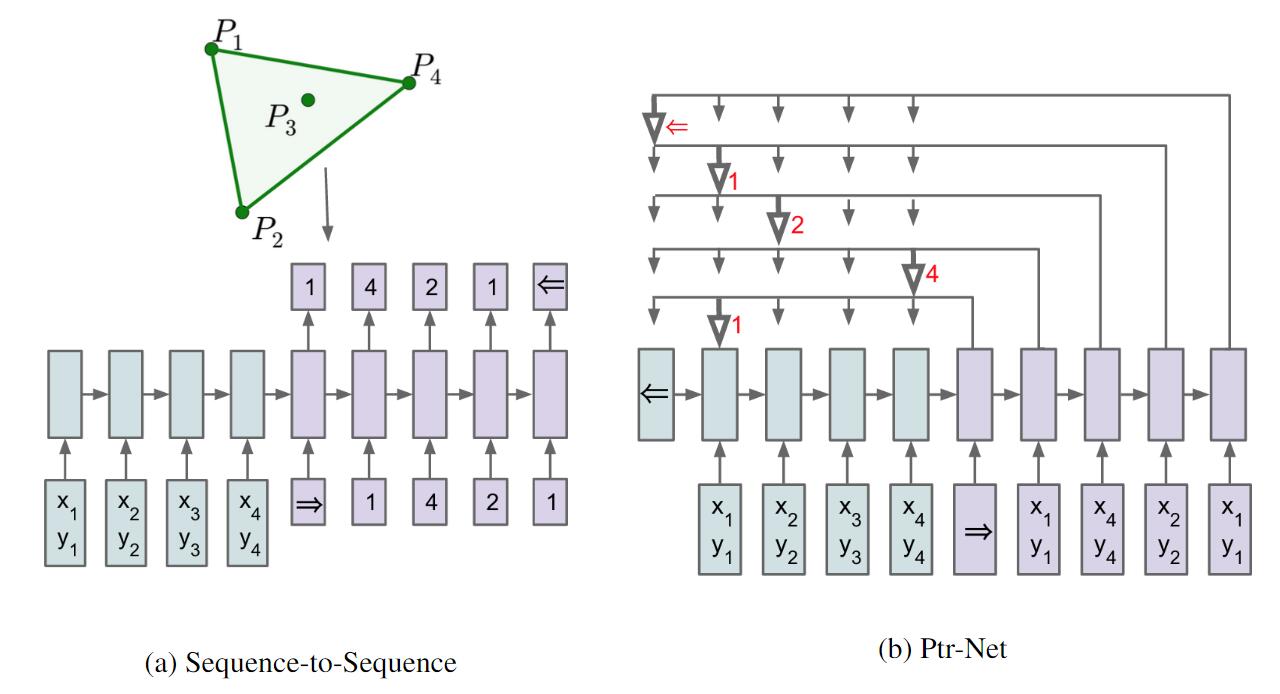
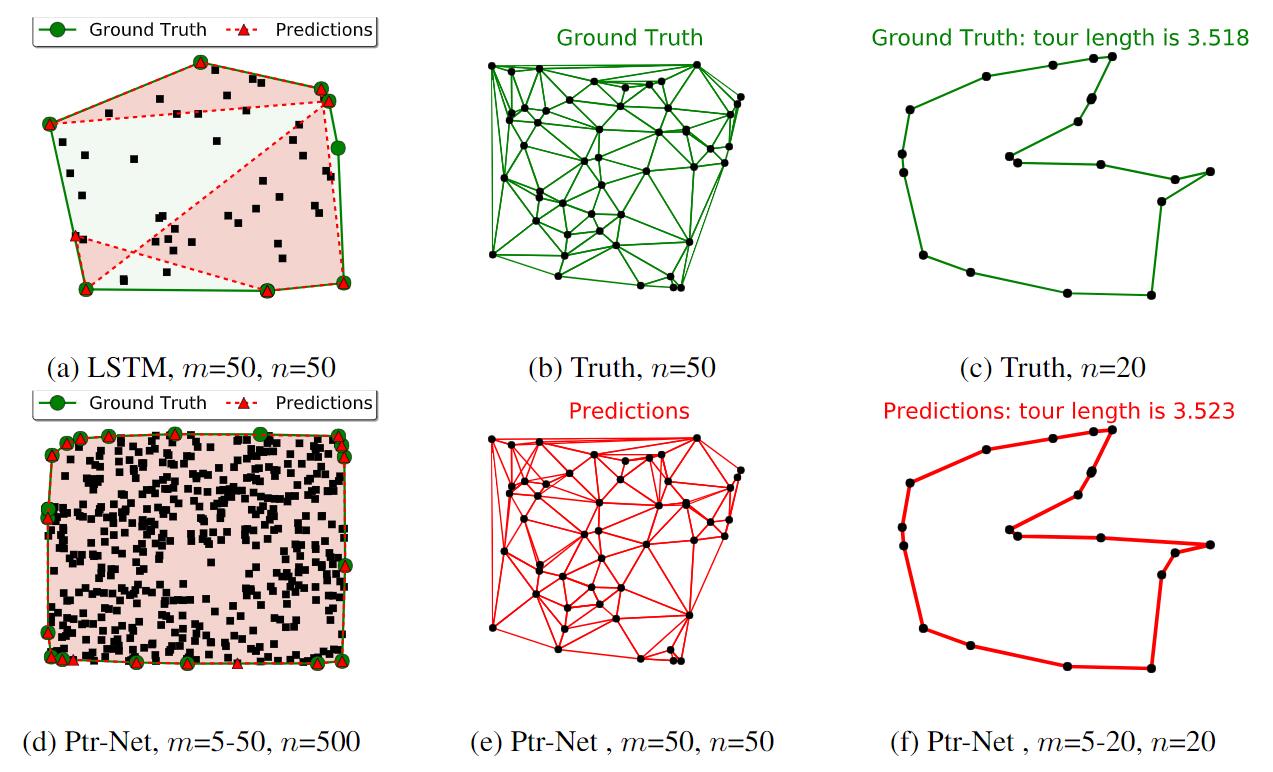
实际上这种结构不仅仅能用于解决凸包问题, 作者还在论文中给出利用Ptr - Net 解决三角形分割(Delaunay Triangulation), 旅行商问题(Travelling Salesman Problem). 作者在调整参数后, 取得了比LSTM好得多的结果:
指针网络因为具有解决输出严重依赖输入问题的能力, 如果应用于NLP的摘要生成任务中, 可以从原文中复现重要的细节, 在某些程度上解决预训练词典大小不足的问题(也称为OOV问题, 即Out of Vocabulary). 虽然这种结构在处理特定问题上有了优势, 但仍然受结构局限, 无法完全应用到通用任务当中.
CopyNet
CopyNet出自论文Incorporating Copying Mechanism in Sequence-to-Sequence Learning. 该论文作者将PtrNet使用于文本摘要提取和对话任务当中.

在原文中作者提到Copy机制与Seq2Seq结合的难点:
From a cognitive perspective, the copying mechanism is related to rote memorization, requiring less understanding but ensuring high literal fidelity. From a modeling perspective, the copying operations are more rigid and symbolic, making it more difficult than soft attention mechanism to integrate into a fully differentiable neural model.
- 从认知角度来看, Copy与死记硬背有关, 不需要理解, 但复制可以确保很高的字面保真度.
- 从建模角度来看, Copy更加僵化和符号化, 使其比软注意力机制更难集成到完全可区分的神经模型中.
因此, 作者提出了另一种复制机制, 能够端到端的只通过梯度下降训练Seq2Seq模型.
前面提到的指针网络只能重复原文内容, 而非从已有的字典中提取内容, 天生就受到了极大的限制. 如果想要破除这种劣势, 就必须让之前的对话生成结构与这种Pointer(或者说Copy)机制相结合.
注: Copy和Pointer的作用都是一致的, 都是将某个时刻的输出调整为先前某个时刻的输入, Copy也是将先前输入作为输出, 指针也是同样效果.
在摘要生成中, 通过复现原文内容的摘要生成称为”抽取式“摘要生成, 而从外部词典中取出的内容叫”生成式“摘要生成. 而作者用复制机制将这两种方式实现了软结合.
沿用Seq2Seq结构, 仍然分为Encoder和Decoder两个部分.
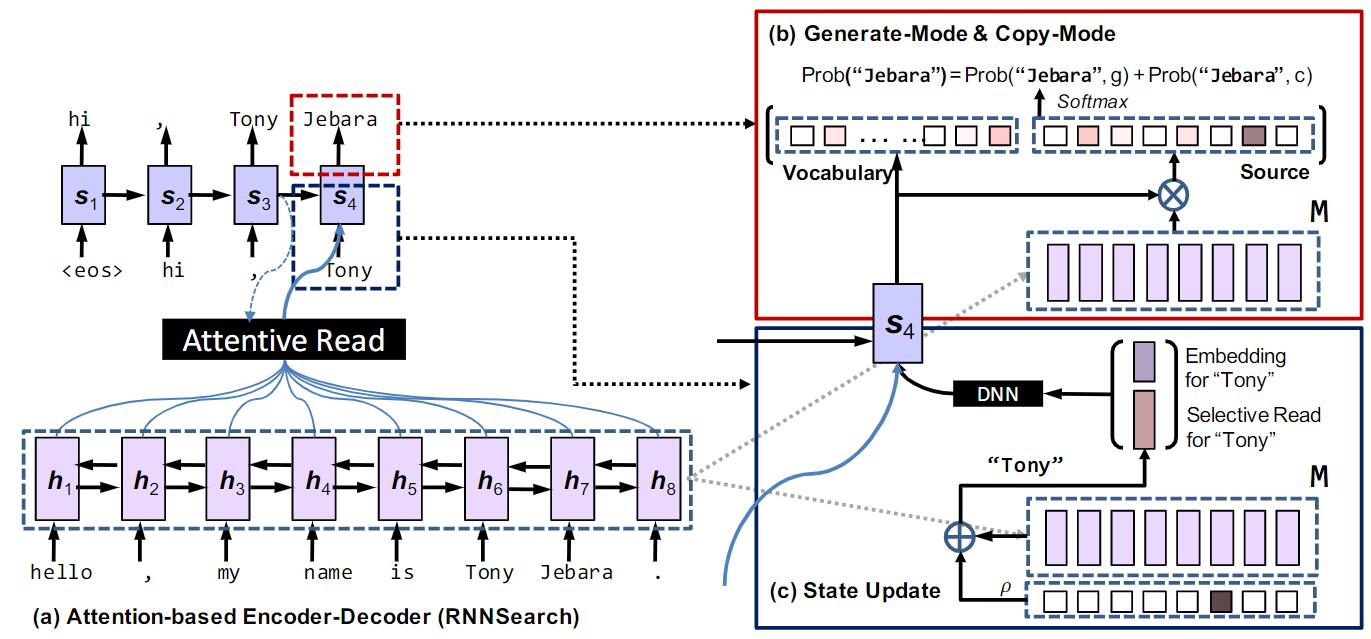
Encoder
Encoder采用双向RNN提取句子信息, 并将每个时刻与输入$x_t$ 相对应的hidden state集合$\left\{\mathbf{h}_{1}, \ldots, \mathbf{h}_{T_{S}}\right\}$ 称为短期记忆$\mathrm{M}$ .
Decoder
Predition
作者将预测分为生成模式和复制模式两种, 当前时刻的预测结果应该是两种模式混合的结果. g代表生成模式, c代表copy模式. 而每个模式的预测结果由Decoder在当前时刻的隐藏状态输出$s_t$, 上个时刻的预测结果$y_{t-1}$, Attention生成的当前时刻的上下文向量$c_t$, 以及短时记忆$\mathrm{M}$ 共同决定.
$$
\begin{array}{r}
p\left(y_{t} \mid \mathbf{s}_{t}, y_{t-1}, \mathbf{c}_{t}, \mathbf{M}\right)=p\left(y_{t}, g \mid \mathbf{s}_{t}, y_{t-1}, \mathbf{c}_{t}, \mathbf{M}\right)
+p\left(y_{t}, c \mid \mathbf{s}_{t}, y_{t-1}, \mathbf{c}_{t}, \mathbf{M}\right)
\end{array}
$$
作者将词语分为在词典中的词语集合$\mathcal{V}=\left\{v_{1}, \ldots, v_{N}\right\}$, 源序列的单词集合$X=\left\{x_{1}, \ldots, x_{T_{S}}\right\}$, OOV单词记为$\mathrm{UNK}$, 每个模式生成的结果计算方式如下:
$$
\begin{array}{l}
p\left(y_{t}, g \mid \cdot\right)=\left\{\begin{array}{cc}
\frac{1}{Z} e^{\psi_{g}\left(y_{t}\right)}, & y_{t} \in \mathcal{V} \\
0, & y_{t} \in \mathcal{X} \cap \bar{V} \\
\frac{1}{Z} e^{\psi_{g}(\mathrm{UNK})} & y_{t} \notin \mathcal{V} \cup \mathcal{X}
\end{array}\right. \\
p\left(y_{t}, \mathrm{c} \mid \cdot\right)=\left\{\begin{array}{cc}
\frac{1}{Z} \sum_{j: x_{j}=y_{t}} e^{\psi_{c}\left(x_{j}\right)}, & y_{t} \in \mathcal{X} \\
0 & \text { otherwise }
\end{array}\right.
\end{array}
$$
其中$Z$ 为生成模式和copy模式共享的归一化项, 作者通过设计归一化项让两种模式通过Softmax来互相竞争(将其代入原式的分母中就是Softmax的形式):
$$
Z=\sum_{v \in \mathcal{V} \cup\{\mathrm{UNK}\}} e^{\psi_{g}(v)}+\sum_{x \in X} e^{\psi_{c}(x)}
$$
$\psi_{g}(\cdot)$ 和 $\psi_{c}(\cdot)$ 是两种打分函数, 会在后面提到如何计算.
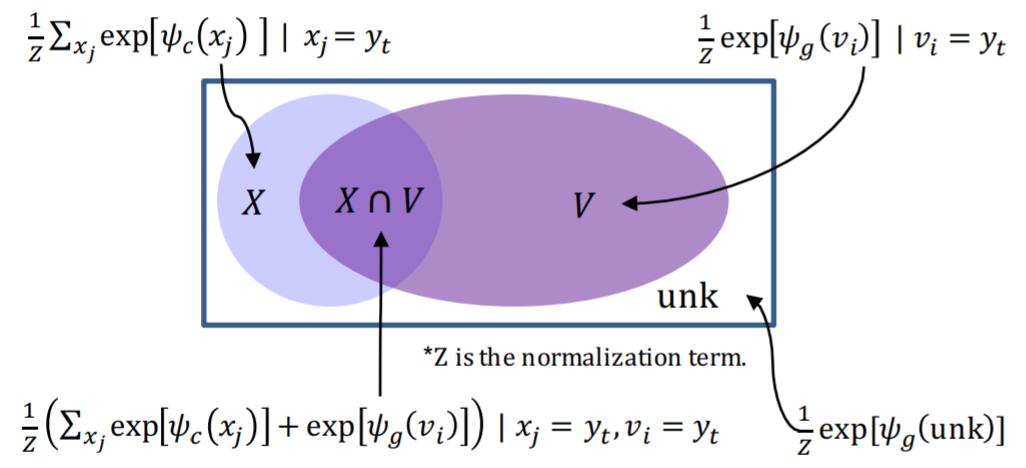
作者还给出了图加以辅助说明计算概率时所对应的不同情况:
生成模式下采用Attention, 打分公式为:
$$
\psi_{g}\left(y_{t}=v_{i}\right)=\mathbf{v}_{i}^{\top} \mathbf{W}_{o} \mathbf{s}_{t}, \quad v_{i} \in \mathcal{V} \cup \mathrm{UNK}
$$
$W_o$ 和$\mathbf{v}_{i}$ 相乘后能获得$v_i$ 的独热编码, 它与$s_t$ 乘后得到一个分数.
copy模式下, 打分公式为:
$$
\psi_{c}\left(y_{t}=x_{j}\right)=\sigma\left(\mathbf{h}_{j}^{\top} \mathbf{W}_{c}\right) \mathbf{s}_{t}, \quad x_{j} \in \mathcal{X}
$$
$W_c$ 是训练得到的, 与$\mathbf h_j$ 相乘经过$\sigma$ (原文使用的是tanh)添加非线性, 将$h_j$ 和 $s_t$ 投射到同一个语义空间.
综上, 当$y_t$ 没出现在源序列中时, $p\left(y_{t}, c \mid \cdot\right)=0$, 只启动生成模式, 当$y_t$ 只出现在源序列时, $p\left(y_{t}, g \mid \cdot\right)=0$, 只启动copy模式.
State Update and Reading M
作者在copy机制下对Decoder的状态更新做了改良, 普通Decoder的状态更新为:
$$
\begin{array}{l}
\mathbf{s}_{t}=f\left(y_{t-1}, \mathbf{s}_{t-1}, \mathbf{c}\right) \\
p\left(y_{t} \mid y_{<t}, X\right)=g\left(y_{t-1}, \mathbf{s}_{t}, \mathbf{c}\right)
\end{array}
$$
作者将$y_{t-1}$ 用$y_{t-1}$ 的Embedding $\mathbf{e}(y_{t-1})$ 和$\zeta\left(y_{t-1}\right)$ 来表示, 并将其concat起来, 即:
$$
\left[\mathbf{e}\left(y_{t-1}\right) ; \zeta\left(y_{t-1}\right)\right]^{\top}
$$
因为使用的是双向RNN, 所以$\mathrm M$ 中既包含了上下文信息, 也包含了位置信息, 这对状态更新很重要, $\zeta\left(y_{t-1}\right)$ 是其中的核心内容, 计算方式如下:
$$
\begin{array}{l}
\zeta\left(y_{t-1}\right)=\sum_{\tau=1}^{T_{S}} \rho_{t \tau} \mathbf{h}_{\tau} \\
\rho_{t \tau}=\left\{\begin{array}{cc}
\frac{1}{K} p\left(x_{\tau}, \mathrm{c} \mid \mathbf{s}_{t-1}, \mathbf{M}\right), & x_{\tau}=y_{t-1} \\
0 & \text { otherwise }
\end{array}\right. \\
K = \sum_{\tau^{\prime}: x_{\tau^{\prime}}=y_{t-1}} p\left(x_{\tau^{\prime}}, c \mid \mathbf{s}_{t-1}, \mathbf{M}\right)
\end{array}
$$
$K$ 是归一化项, 作者将这个过程称为Selective Read, 即用$\zeta\left(y_{t-1}\right)$ 对$\mathbf h_\tau$ 进行加权求和. 从式子直观上来理解, 仅当Encoder接受的输入在上个Decoder输出时刻相同时, 这个$\rho$ 才有意义. 通过这种方式, 对于在前文已经出现的单词, Decoder就能拿到额外的上下文信息和位置信息. 一旦$\zeta$ 有值, 当前时刻的输出就会倾向于copy模式, 因为上个时刻的输出在原文中能够找到, 那么当前时刻的内容也有相当大的概率从原文中copy.
这个$\zeta$ 似乎和$c_t$ 差不多, 不知道有没有信息上的冗余.
综上, 将更新过程总结如下:
$$
\zeta\left(y_{t-1}\right) \stackrel{\text { update }}{\longrightarrow} \mathbf{s}_{t} \stackrel{\text { predict }}{\longrightarrow} y_{t} \stackrel{\text { sel. read }}{\longrightarrow} \zeta\left(y_{t}\right)
$$
在原文中最后的实验对比结果中. CopyNet对于Copy任务做的效果都碾压基础模型, 但唯独对于结束符的生成准确率较差, 这也为大量生成重复内容埋下了隐患.
Pointer - Generator Network
指针生成网络受到了PtrNet和CopyNet的影响, 仍然沿用原输入的复现能力与基于已有知识的文本生成能力做结合的思路, 并针对指针生成网络出现的问题做了改进. 与CopyNet相比更加简洁.
该结构出自Get To The Point: Summarization with Pointer-Generator Networks, 这是一篇非常不错的论文, 如果时间不充裕我建议阅读这篇, 作者逻辑清晰, 图片也简单易懂.
该模型应用于摘要生成任务中, 作者在论文开头便提出了现存模型在摘要生成中出现的问题:

- 对于图中的红色字, 存在内容抽取不准确的情况.
- 对于图中的绿色字, 存在多次与原文中生成重复且无意义内容的情况.
指针生成网络沿用了CopyNet生成式和抽取式并存的思想, 分为抽取式摘要生成和基于单词表的生成式摘要生成, 并可以在生成模式和抽取模式之间更灵活的切换.
Our pointer-generator network is a hybrid betweenour baseline and a pointer network, as it allows both copying words via pointing, and generating words from a fixed vocabulary.
Baseline
在原论文中, 作者用标准的Seq2Seq + Attention作为Baseline:

这是一种非常直觉性的办法. Seq2Seq架构下用双向RNN提取隐藏状态$h_i$, Decoder解码得到$s_t$, 用Bahdanau Attention提取上下文信息$h^\ast_t$:
$$
\begin{array}{l}
e_{i}^{t}=v^{T} \tanh \left(W_{h} h_{i}+W_{s} s_{t}+b_{\text {attn }}\right) \\
a^{t}=\operatorname{softmax}\left(e^{t}\right) \\
h_{t}^{\ast}=\sum_{i} a_{i}^{t} h_{i}
\end{array}
$$
然后根据得出的上下文信息和Decoder当前时刻解码信息, 经过Softmax得到当前时刻的词语概率分布$P_{\text {vocab }}$:
$$
P_{\text {vocab }}=\operatorname{softmax}\left(V^{\prime}\left(V\left[s_{t}, h_{t}^{\ast}\right]+b\right)+b^{\prime}\right)
$$
为了后面体现出指针生成网络和Baseline的差异, 直接令$P_{\text{vocab}}$就是最终结果:
$$
P(w)=P_{\text {vocab }}(w)
$$
然后用对数似然做损失, 计算总共的Loss:
$$
\begin{aligned}
\operatorname{loss}_{t}&=-\log P\left(w_{t}^{\ast}\right) \\
\operatorname{loss}&=\frac{1}{T} \sum_{t=0}^{T} \operatorname{loss}_{t}
\end{aligned}
$$
Pointer - Generator Network
作者基于Baseline的缺点, 给出了指针生成网络:
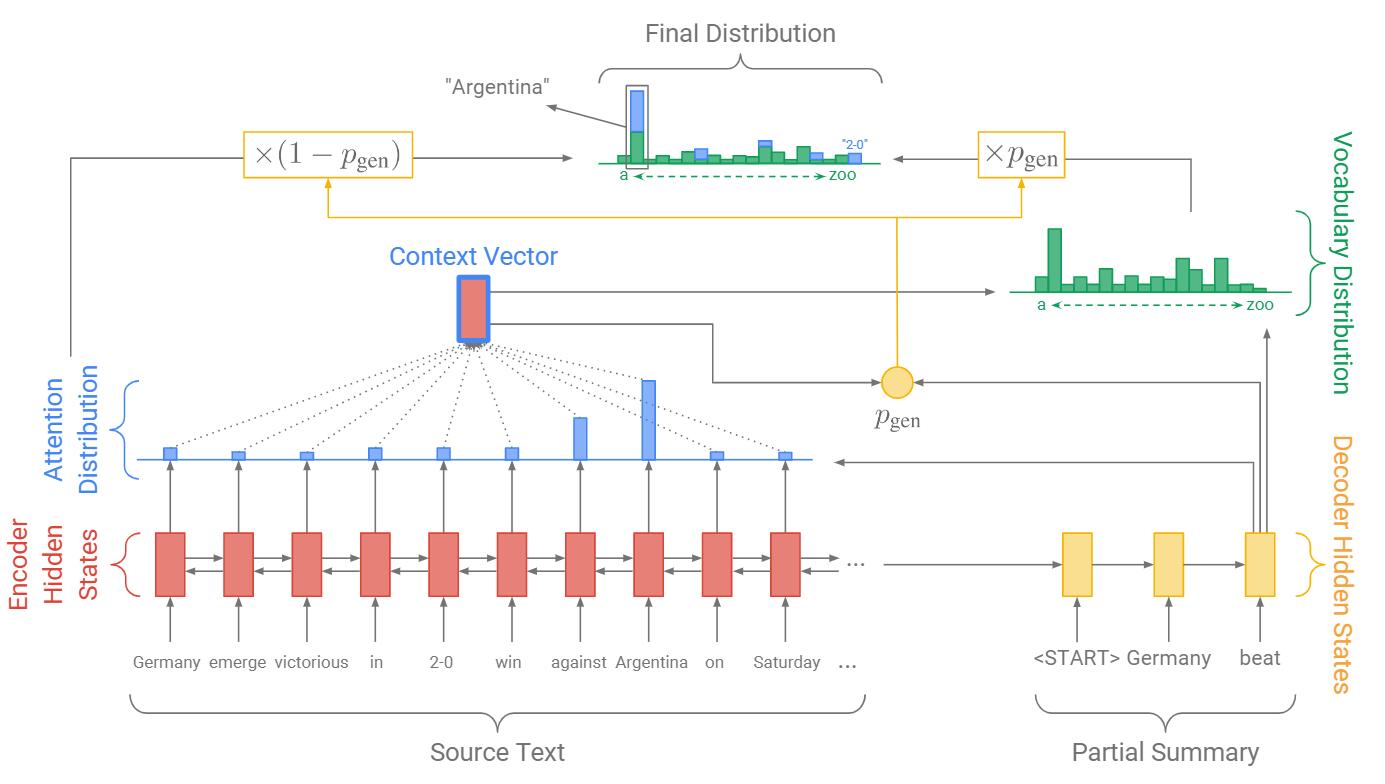
与Baseline的图相对比, 最大的变化就是多了一个$p_{\text{gen}}$, 导致有其他很多连带的内容不同.
和之前一样, 我们仍然计算Attention和绿色对应的词表概率分布, 但同时根据当前时刻Decoder的输入$x_t$ 能额外得到一个概率$p_{\text{gen}} \in [0, 1]$:
$$
p_{\mathrm{gen}}=\sigma\left(w_{h^{\ast}}^{T} h_{t}^{\ast}+w_{s}^{T} s_{t}+w_{x}^{T} x_{t}+b_{\mathrm{ptr}}\right)
$$
引入$p_{\text{gen}}$ 就是想在Baseline的基础上将生成式与抽取式利用开关做个软结合, 从而改善最终结果:
$$
P(w)=p_{\mathrm{gen}} P_{\mathrm{vocab}}(w)+\left(1-p_{\mathrm{gen}}\right) \sum_{i: w_{i}=w} a_{i}^{t}
$$
生成模式的概率是$p_{\text{gen}}$, 那么copy模式的概率就是$1 - p_{\text{gen}}$. copy模式中用到了$a^t$, 当单词$w$ 在之前的输入中出现过时候, 我们将其Attention累加起来, 所以在原文中出现次数越多的词使用copy模式的概率就越大, 被添入摘要的概率也就越大. 如果$w$ 直接OOV了, 则$P_{\mathrm{vocab}}(w)=0$, 如果$w$ 没在原文中出现, 那么令$\sum_{i: w_{i}=w} a_{i}^{t}=0$.
模型非常简单, 图画的也特别好, 以至于让人一目了然.
Coverage Mechanism
覆盖(汇聚?)机制与指针生成网络出自同一篇论文. 在原文中作者提到:
Repetition is a common problem for sequence-to-sequence models, and is especially pronounced when generating multi-sentence text. We adapt the coverage model of Tu et al. (2016) to solve the problem.
对于Seq2Seq模型来说, 重复是一个非常令人头疼的问题, 作者在指针生成网络的基础上提出了Converage Mechanism. 思想非常简单, 作者通过Coverage Mechanism来记录之前时刻Attention的和, 作为当前时刻对原文单词关注位置的依据, 令其为$c^t$:
$$
c^{t}=\sum_{t^{\prime}=0}^{t-1} a^{t^{\prime}}
$$
注: 这里的$c^t$ 不是上下文关系, 而是coverage vector, 在本论文中采用$h_t^{\ast}$ 作为上下文关系.
$c^t$ 代表了先前模型对这些单词关注的覆盖程度(不知道是不是”覆盖”二字的来源), 模型先前越有可能copy过, 那么覆盖向量就越大.
将Coverage Mechanism加入Attention中去, 将模型对单词的关注程度也作为Attention的依据:
$$
e_{i}^{t}=v^{T} \tanh \left(W_{h} h_{i}+W_{s} s_{t}+w_{c} c_{i}^{t}+b_{\mathrm{attn}}\right)
$$
单单影响Attention不能产生太大作用, 因为模型并不知道要往哪个方向进行优化, 还需要给模型一个引导, 将相关的内容作为Loss体现:
$$
\displaylines{
\operatorname{covloss}_{t}=\sum_{i} \min \left(a_{i}^{t}, c_{i}^{t}\right) \\
\operatorname{covloss}_{t} \leq \sum_{i} a_{i}^{t}=1
}
$$
$\text{covloss}$ 使得模型更容易选择不同的单词做copy, 而非大量重复copy. 若重复copy, $a^t$ 和 $c^t$ 都会很高, 模型会被惩罚的更严重.
令$\lambda$ 为超参数加权, 将$\text{covloss}$ 加入总体损失中:
$$
\operatorname{loss}_{t}=-\log P\left(w_{t}^{\ast}\right)+\lambda \sum_{i} \min \left(a_{i}^{t}, c_{i}^{t}\right)
$$

