不要再对类别变量独热编码

本文参考了Stop One-Hot Encoding Your Categorical Variables, 并对其内容在加以自身理解的情况下进行翻译.

独热编码

对不同的类别变量就需要用到独热编码, 独热编码是将类别变量映射为离散型特征的方法. 由于类别变量经常是以字符串类型存在的, 这是不能被机器所量化接受的, 必须通过某种方式映射成机器可以接受的数值才能够运算.

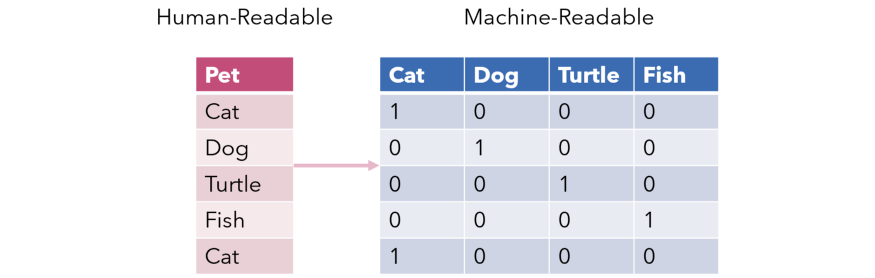
当类别比较多时, 独热编码产生的向量是非常巨大的稀疏向量, 这些增加进去的维度为问题扩大了搜索空间, 同时因为向量的稀疏性引入了很多不必要的计算, 提升了解决问题的难度. 因此在能够解决问题的情况下, 最好维持足够少的特征维度, 以保证任务在有限时间内解决的可行性. 尤其是对于神经网络, 独热编码有明显的副作用.

更麻烦的是由于独热编码是对类别变量加工产生稀疏向量的特性, 还会导致这些被编码的特征之间产生多重共线性, 即产生的稀疏特征向量线性相关, 在优化过程中就使得对这些稀疏向量之间互相依赖, 难以优化. 除非是算法对稀疏有优化, 否则对于较少的类别变量不会引入太大的问题, 一旦问题具备一定规模就会带来很大的危害.

目标编码

目标编码是表示类别的一种有效方法, 只占用一个维度的特征. 它也被称为均值编码, 这种方法更好的表示类别变量和目标之间的关系, 在Kaggle中非常常见.

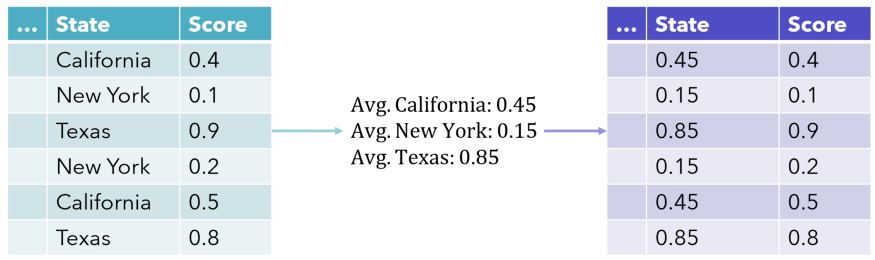
对于上图来说, 简单点的做法它是将相同类别变量的Score 相加并求均值.

更普适的方法是利用样本的先验概率和后验概率结合权重函数形成一个凸组合来得到均值, 假设分类问题需要分出C个不同的类别, 那么对于要区分的每个类别, 都能有与之相对应的类别变量形成的均值特征.

由于区分的每个类别概率和为1, 在区分最后一个类时, 其概率一定与前面形成的特征线性相关, 所以可以舍弃它. 整个数据集就扩充了C-1列, 而不是C列.

更加详细的就不介绍了, 可以看特征编码总结 Kaggle 或者平均数编码：针对高基数定性特征（类别特征）的数据预处理/特征工程了解更多.

但这种方法也有缺点:

模型更难学习均值编码和其他变量之间的关系, 它只与
对模型的标签极为敏感, 因为编码是与模型标签相关的, 如果数据集标签有细微变化, 都可能导致编码出现问题, 进而影响预测效果. 所以异常值对它影响非常大.
可能加剧过拟合. 因为均值编码是连续值, 在过拟合时可能将差别很小的两个编码样本认为是完全不同的两个类.

category_encoders 已经以sklearn的方式对这种编码进行了封装, 因为目标编码是一种监督学习编码, 所以必须同时传入X和Y.

from category_encoders import TargetEncoder
encoder = TargetEncoder(cols=['Name_of_col', 'Another_name'])
train_data = encoder.fit_transform(X_train, y_train)

留一编码

留一编码通过排除当前行的值来计算均值来作为编码, 使得数值更加多样化, 一定程度上减轻了编码对标签的依赖.

这个方法能够将类别变量映射到某个范围内, 而并非某个具体值. 例如图中的State=California 有0.5和0.4两种不同的取值, 所以泛化能力会更好.

同样使用category_encoders 实现.

from category_encoders import LeaveOneOutEncoder
encoder = LeaveOneOutEncoder(cols=['Name_of_col','Another_name'])
train_data = encoder.fit_transform(X_train, y_train)

与留一法效果相似的一种方法是在编码中加入正态分布的噪声, 并将标准差作为一个可以调节的参数.

贝叶斯目标编码

贝叶斯目标编码的可解释性更差, 因为它是一种更偏向数学的方法. 它认为均值作为度量可能存在一定欺骗性, 因此应该加入其它的统计量进行运算, 例如方差和偏度. 然后通过贝叶斯模型将这些统计变量的分布属性纳入其中, 从而产生更贴近类别标签的分布编码.

证据权重

证据权重是对分类独立变量和因变量之间的关系的另一种更微妙的表现. Weight of Evidence(WoE) 是从信用评分领域演变来的, 曾被用于衡量违约用户和还款用户间的差异. 证据权重的数学定义是几率比的自然对数, 即不属于某个类的百分比和属于某个类的百分比之差的对数. 并且WoE是IV值的关键组件.

实现仍然是通过category_encoders:

from category_encoders import WOEEncoder
encoder = WOEEncoder(cols=['Name_of_col','Another_name'])
train_data = encoder.fit_transform(X_train, y_train)