2020.09.08: 更新了剪枝.
决策树DT Desicion Tree
决策树(Decision Tree) 是在已知各种情况发生概率的基础上, 通过构成决策树来求取净现值的期望值大于等于零的概率, 评价项目风险, 判断其可行性的决策分析方法, 是直观运用概率分析的一种图解法. 由于这种决策分支画成图形很像一棵树的枝干, 故称决策树. 在机器学习中, 决策树是一个预测模型, 他代表的是对象属性与对象值之间的一种映射关系. Entropy = 系统的凌乱程度, 使用算法ID3, C4.5和C5.0生成树算法使用熵. 这一度量是基于信息学理论中熵的概念. 决策树是一种树形结构, 其中每个内部节点表示一个属性上的测试, 每个分支代表一个测试输出, 每个叶节点代表一种类别.
相关概念
决策树分为两种, 也就是按照它们功能进行区分的, 回归树和分类树. 决策树作为树类模型, 不依赖于特征的离散或连续, 树的分裂仅取决于分裂时的判断条件, 与特征的离散或连续性无关.
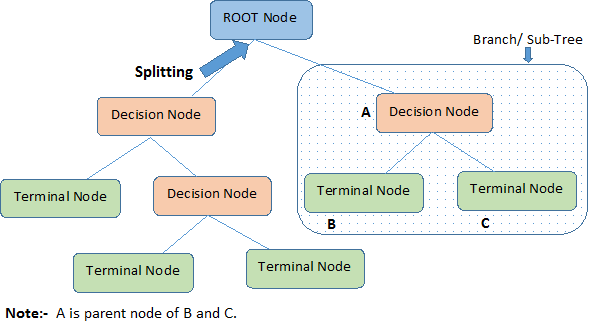
- 根结点(Root Node): 它表示整个样本集合, 并且该节点可以进一步划分成两个或多个子集.
- 拆分(Splitting): 表示将一个结点拆分成多个子集的过程.
- 决策结点(Decision Node): 当一个子结点进一步被拆分成多个子节点时, 这个子节点就叫做决策结点.
- 叶子结点(Leaf/Terminal Node): 无法再拆分的结点被称为叶子结点.
- 剪枝(Pruning): 移除决策树中子结点的过程就叫做剪枝, 跟拆分过程相反.
- 分支/子树(Branch/Sub-Tree): 一棵决策树的一部分就叫做分支或子树.
- 父结点和子结点(Paren and Child Node): 一个结点被拆分成多个子节点, 这个结点就叫做父节点;其拆分后的子结点也叫做子结点.
构造过程
决策树的构造过程一般分为3个部分, 分别是特征选择, 决策树生产和决策树裁剪.
特征选择
特征选择表示从众多的特征中选择一个特征作为当前节点分裂的标准, 如何选择特征有不同的量化评估方法, 从而衍生出不同的决策树, 如ID3(通过信息增益选择特征) , C4.5(通过信息增益比选择特征) , CART(通过Gini指数选择特征) 等.
目的(准则) : 使用某特征对数据集划分之后, 各数据子集的纯度要比划分钱的数据集D的纯度高(也就是不确定性要比划分前数据集D的不确定性低.
决策树的生成
根据选择的特征评估标准, 从上至下递归地生成子节点, 直到数据集不可分则停止决策树停止生长. 这个过程实际上就是使用满足划分准则的特征不断的将数据集划分成纯度更高, 不确定行更小的子集的过程. 对于当前数据集的每一次划分, 都希望根据某个特征划分之后的各个子集的纯度更高, 不确定性更小.
决策树的裁剪
决策树容易过拟合, 一般需要剪枝来缩小树结构规模, 缓解过拟合.
划分选择
划分选择是决策树进行学习的关键. 我们希望决策树的分支节点包含的样本尽可能属于同一类别, 即节点的纯度越来越高, 选择方法都是基于最大熵原理的. 最大熵原理是一种选择随机变量统计特性最符合客观情况的准则, 也称为最大信息原理, 在已知一些知识的情况下, 将其他所有未知的事件全部当做等概率事件来处理. 万物趋近于无序, 当事件越不确定(等事件概率发生)时, 熵就最大.
信息增益 Information Gain
信息熵是度量样本集合纯度的一种常用指标. 对于当前样本集合$D$中第$k$类样本所占的比例$p_k$, 其信息熵定义为:
$$
{\rm Ent}(D) = - \sum_k^{K}p_k \log_2{p_k}
$$
熵越小, 未知的信息就越少, 即纯度越高. 这里约定如果$p=0$, 则$p\log_2p=0$ .
而在节点划分时, 可能特征$a$有多个可以取到的可能性$V$, 对数据集进行划分, 这时候可以用条件熵是用来表示在这个特征下某值的不确定性. 这里的${\rm Ent}(D^v)$ 其实就是${\rm Ent}(D|a=a_v)$. 为了保证后续和西瓜书上的公式形式一致采取了前者.
$$
{\rm Ent}(D|a)=\sum_{v=1}^V\frac{|D^v|}{|D|}{\rm Ent}(D^v)
$$
信息增益就是在按照特征的某值进行划分后的熵的变化, 条件熵越大, 证明划分效果越差, 对应的信息增益就越少:
$$
{\rm Gain}(D, a) ={\rm Ent}(D)-{\rm Ent}(D|a)
$$
使用信息增益作为节点划分依据的算法称为ID3算法.
以周志华老师的西瓜书中的西瓜数据集为例:
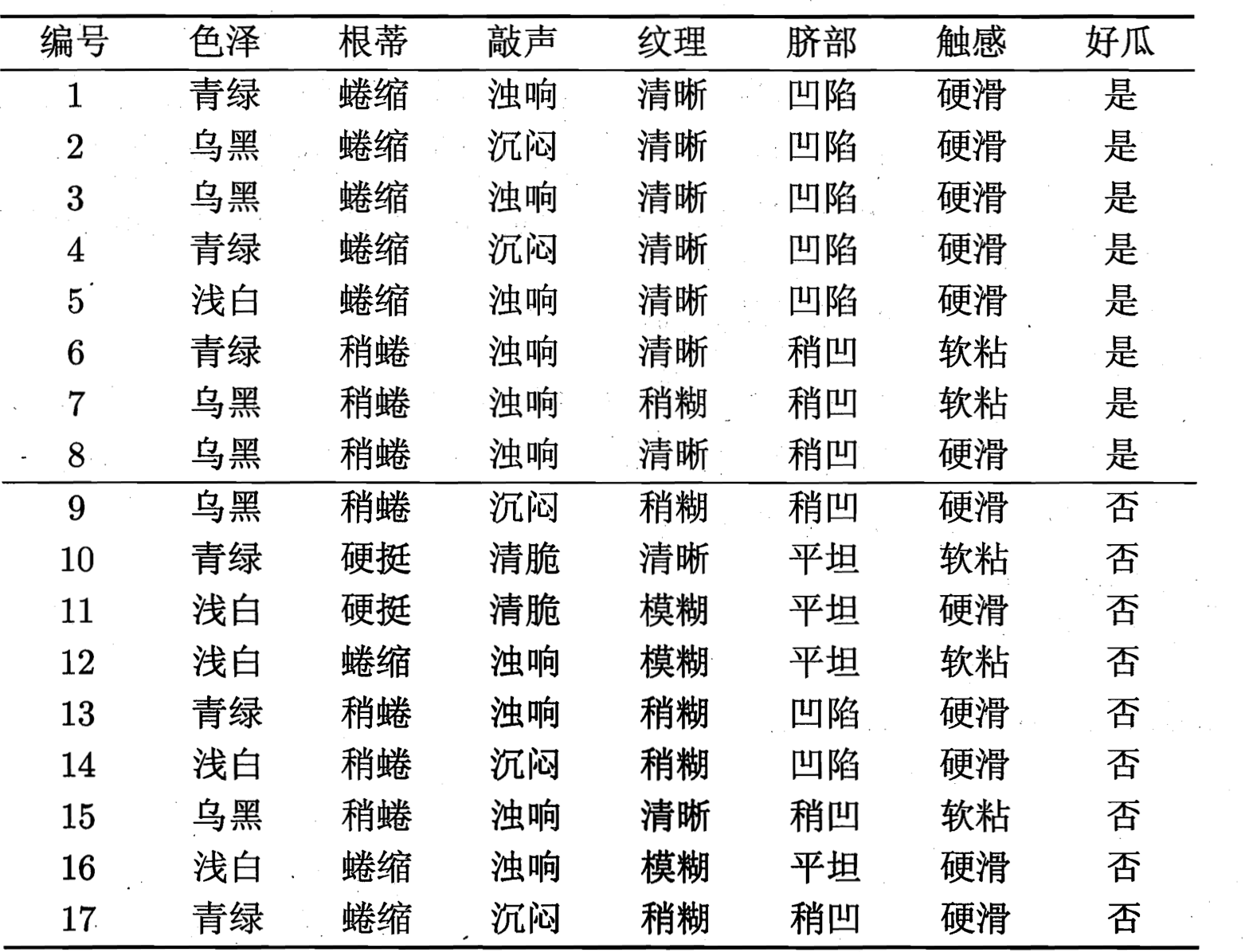
明显西瓜只有好瓜和坏瓜两种, 好瓜$p_1=\frac{8}{17}$. 坏瓜$p_2=\frac{9}{17}$首先计算出根节点的信息熵:
$$
{\rm Ent}(D) = - \sum_{k=1}^{2}p_k \log_2{p_k}=-(\frac{8}{17}\log_2\frac{8}{17}+\frac{9}{17}\log_2\frac{9}{17})=0.998
$$
然后要遍历当前的属性集合$\{色泽, 根蒂, 敲声, 纹理, 脐部, 触感\}$. 以色泽为例, 有三个可能取值$\{青绿, 乌黑, 浅白\}$. 将这个属性进行划分, $D^1(色泽=青绿)$, $D^2(色泽=乌黑)$, $D^3(色泽=浅白)$. 对于子集$D^1, p_1=\frac{3}{6}, p_2=\frac{3}{6}$, 对于子集$D^2, p_1=\frac{4}{6}, p_2=\frac{2}{6}$, 对于子集$D^3, p_1=\frac{1}{5}, p_2=\frac{4}{5}$, 以色泽为划分依据之后得到三个节点的信息熵为:
$$
\begin{aligned}
{\rm Ent}(D^1)&=-(\frac{3}{6}\log_2\frac{3}{6}+\frac{3}{6}\log_2\frac{3}{6})=1 \\
{\rm Ent}(D^2)&=-(\frac{4}{6}\log_2\frac{4}{6}+\frac{2}{6}\log_2\frac{2}{6})=0.918 \\
{\rm Ent}(D^3)&=-(\frac{1}{5}\log_2\frac{1}{5}+\frac{4}{5}\log_2\frac{4}{5})=0.722 \\
\end{aligned}
$$
因此能够根据信息熵计算出信息增益为:
$$
\begin{aligned}
{\rm Gain}(D, 色泽)&={\rm Ent}(D)-\sum_{v=1}^3\frac{|D^v|}{|D|}{\rm Ent}(D^v)\\
&=0.998-(\frac{6}{17}\times 1 + \frac{6}{17} \times 0.918 + \frac{5}{17}\times 0.722) \\
&=0.109
\end{aligned}
$$
信息增益比 Information Gain Ratio
不要忘记西瓜数据集中, 仍然含有”编号”这一特征, 如果将其作为特征纳入决策树的选择中, 那岂不是决策树可以完美拟合编号这一特征, 而完全丧失了泛化能力? 其实对于其他取值较多的特征亦是如此, 当特征的可能性较多时, 每次做一次节点划分, 信息增益会偏爱那些取值多的特征, 因为原本特征的不确定性就比较大, 所以当选择一个值作为划分时, 消除的熵也很多, 信息增益就会变得大.
这时就需要用某种熵的定义来平衡掉这个偏好, 也就是”信息增益率”.
$$
{\rm Gain\_ratio}(D, a) = \frac{ {\rm Gain}(D, a)} { {\rm IV}(a)}
$$
其中有:
$$
{\rm IV}(a) = -\sum_{v=1}^V\frac{|D^v|}{|D|}\log_2 \frac{|D^v|}{|D|}
$$
$a$ 的可能取值数目越多, 则${\rm IV}(a)$就越大(其实它完全就是按照熵来定义的, 不确定性越多熵越大). 但是信息增益率可能对取值数目少的特征有所偏好, 因此是先从候选划分属性中找出信息增益高于平均水平的属性, 然后再从中选择增益率最高的.
使用信息增益比作为节点划分依据的算法称为C4.5算法.
基尼指数 Gini Index
基尼值表示了数据集的纯度, 因此划分准则可以用基尼指数:
$$
\begin{aligned}
{\rm Gini}(D)&=\sum_{k=1}^K\sum_{k’\neq k}p_kp_{k’} \\
&=1-\sum_{k=1}^Kp_k^2
\end{aligned}
$$
某个属性的基尼指数定义为:
$$
{\rm Gini\_index}(D,a)=\sum_{v=1}^{V}\frac{|D^v|}{|D|}{\rm Gini}(D^v)
$$
其实和之前的条件熵的形式如出一辙. 因此我们在选择候选属性时, 选择划分后基尼指数最小的属性为最优划分属性.
使用信息增益比作为节点划分依据的算法称为CART算法.
连续值处理
对于连续属性, 可取值书目不再有限, 因此采用最简单的二分法. 对于给定样本中连续属性的所有不同取值, 从小到大进行排序, 然后对每个值进行一次二分, 每次都产生比划分点$t$ 的值不大的集合$D_t^-$和比它大的集合$D_t^+$, 然后再进行计算信息增益, 以信息增益最大的划分点作为划分依据即可.
决策树剪枝
剪枝是决策树缓解过拟合的重要手段, 当决策树对节点划分过于细致时候就容易发生过拟合. 决策树有预剪枝和后剪枝两种剪枝策略, 即分别在决策树构建划分节点时和决策树生长完成后剪枝.
预剪枝
预剪枝基于分支划分的准则, 在局部子树生成完成后, 依据验证集计算节点划分后能否带来收益, 如果没有性能上的提升或者导致性能下降, 则禁止该节点的划分.
除了依据划分准则进行预剪枝外, 还可以设定树的生长高度或导致叶子节点分裂的最小样本数, 禁止节点划分的最小阈值等参数, 达到防止过拟合的效果.
因为预剪枝是与决策树构建并行的, 所以可能会因为局部的性能提升而剪掉更有潜力的节点, 可能过早的停止决策树构造. 常常效果也没有后剪枝好.
后剪枝
等决策树完整生成后, 后剪枝才开始工作. 后剪枝将从决策树的底部往上进行剪枝, 如果剪枝能够提高验证集的精度, 那么就将其裁去. 后剪枝还有许多其他的剪枝方法, 通过采用不同的性能标准来决定节点的保留与否.
后剪枝因为不具有视野上的问题, 保留的分支常比预剪枝要多, 泛化能力也更好一些.
优缺点
优点: 可解释性好, 分类速度快.
缺点: 如果不采用剪枝或随机森林很容易发生过拟合, 体现在决策树结构中就是树划分的过细, 或者深度过深.

