K-means

K-means是一种最为常用的硬聚类算法. 硬聚类指的是分出的样本必须只隶属于某一个类, 而不是给出隶属某几个类的概率.

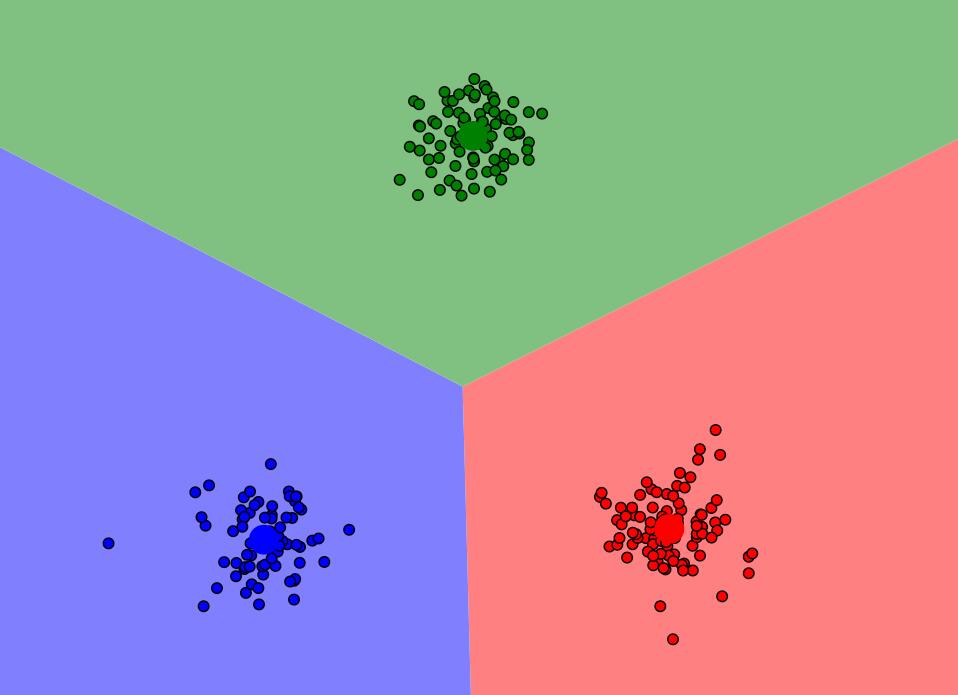
流程

对于给定的$k$类, 聚类所得的簇划分$C_k$, 以及样本$\boldsymbol{x}$, K-means 的目标是最小化平方误差:
$$
E=\sum_{i=1}^{k} \sum_{\boldsymbol{x} \in C_{i}}\mid\mid\boldsymbol{x}-\boldsymbol{\mu}_{i}\mid\mid_{2}^{2}
$$
其中$\mu_i$是簇$C_i$的中心点(或者称为质心):
$$
\mu_i=\frac{1}{\mid C_i\mid}\sum_{\boldsymbol x \in C_i}\boldsymbol x
$$
直观来看, 误差在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度, 误差越小簇内的样本相似度越高. 但是因为求解很难, 所以采用贪心算法通过迭代来近似求解. 具体步骤如下:

从样本集中随机初始化, 随机选择$k$个样本集作为各类(簇)的中心点, $\{\mu_1,\mu_2,\dots, \mu_k\}$.
计算所有样本点与各个簇中心之间的距离, 然后把每个样本点划入离该点最近的簇中.
根据簇中已有的样本点, 重新计算簇中心$\mu_k$.
重复2 - 3, 直到所有的点无法再更新到其他分类或达到最大迭代次数, 算法结束.

缺陷

如果按照上述过程进行求解, 对于一些特殊的情况, 它完全可能会陷入局部最优, 这取决于初始化中心点的初始位置. 有时候甚至能产生反直觉的聚类效果.

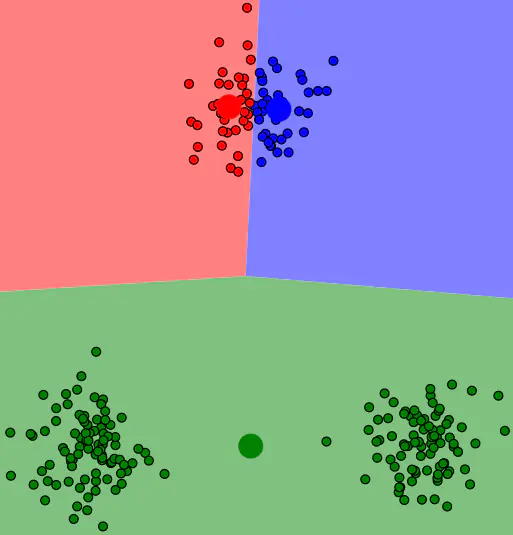
在上图中, 因为随机初始化是一个局部最优情况, 所以下方的两个簇永远都只隶属于绿色, 上方一个簇被强行拆分成了两个簇. 为了尽可能消除这种情况, sklearn中的初始化非常粗暴, 直接随机初始化了若干组中心点, 看哪个效果比较好就采用哪组的结果.

另外, 异常值会使得中心点有很大的变动, 所以K-means对异常值还是非常敏感的. 所以在处理前最好先将异常值去掉.

改进 K-means++

K-means++ 改进了原来的初始化中心点选取方法, 初始聚类中心相互之间应该分得越开越好.

在数据点随机选取一个样本点为第一个簇中心$C_1$.
计算剩余样本与所有簇中心的最短距离$D(x_i)=\min [dist(x_i, C_1), dist(x_i, C_2),\dots, dist(x_i, C_k)]$, 使得这个样本点被选为下一个簇中心的概率$P(x)=\frac{D(x)^{2}}{\sum_{x \in X} D(x)^{2}}$. 按照这个概率随机选取一个中心.
重复步骤2直到选出$k$个簇中心.

样本点离已有的簇中心距离越远, 概率越大, 就越有可能被选为新的簇中心.